Question

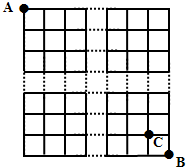如图所示，某城市有南北街道和东西街道各n+1条，一邮递员从该城市西北角的邮局A出发，送信到东南角B地，要求所走路程最短．
（1）求该邮递员途径C地的概率f（n）；
（2）求证：2＜[2f（n）]²ⁿ⁺¹＜3，（n∈N^*）．

Answer 1

分析：（1）求得所走路程最短共有

C

n+1 2n+2

种不同的走法，其中途径C地的走法有2

C

n 2n

种走法，由此可得邮递员途径C地的概率f（n） 的值．
（2）由2f（n）=

2(n+1)

2n+1

=1+

1

2n+1

，得只要证且n≥3 时，2＜(1+

1

n

)n＜3 即可．利用放缩法证明 2＜(1+

1

n

)n，(1+

1

n

)n＜3，从而证明不等式成立．

解答：解：（1）邮递员从该城市西北角的邮局A到达东南角B地，要求所走路程最短共有

C

n+1 2n+2

种不同的走法，其中途径C地的走法有2

C

n 2n

种走法，
所以邮递员途径C地的概率f（n）=

2 C  n 2n

C n+1 2n+2

=

2(2n)!

(n!)2

•

[(n+1)!]2

(2n+2)!

=

n+1

2n+1

．
（2）由2f（n）=

2(n+1)

2n+1

=1+

1

2n+1

，得[2f（n）]²ⁿ⁺¹=(1+

1

2n+1

)2n+1．
要证 n∈N^*时，2＜[2f（n）]²ⁿ⁺¹＜3，
只要证 n∈N^* 时，2＜(1+

1

2n+1

)2n+1＜3，
因为  n∈N^* 时，2n+1∈N^*，且 2n+1≥3，
所以只要证 n∈N^* 时，且n≥3 时，2＜(1+

1

n

)n＜3．  
由于n≥3 时，(1+

1

n

)n=

C

0 n

+

C

1 n

•

1

n

+

C

2 n

•(

1

n

)2+…+

C

n n

•(

1

n

)n＞

C

0 n

+

C

1 n

•

1

n

=2，
且  (1+

1

n

)n=

C

0 n

+

C

1 n

•

1

n

+

C

2 n

•(

1

n

)2+…+

C

n n

•(

1

n

)n=2+

n(n-1)

2!

•

1

n2

+

n(n-1)(n-2)

3!

•

1

n3

+…+

n•(n-1)•(n-2)•3•2•1

n!

•

1

nn

  
=2+

1

2!

•

n

n

•

n-1

n2

+

1

3!

•

n

n

•

n-1

n

•

n-2

n

+…+

1

n!

•

n

n

•

n-1

n

•

n-2

n

…

2

n

•

1

n

＜2+

1

2!

+

1

3!

+…+

1

n!

 
＜2+

1

1×2

+

1

2×3

+

1

3×4

+…+

1

n(n-1)

=2+(

1

1

-

1

2

)+(

1

2

-

1

3

)+(

1

3

-

1

4

)+…+(

1

n-1

-

1

n

)=3-

1

n

＜3． 
综上可得：2＜(1+

1

n

)n＜3 成立，即 2＜[2f（n）]²ⁿ⁺¹＜3成立．

点评：本题主要考查排列、组合以及二项式定理的应用，等可能事件的概率，用放缩法证明不等式，属于难题．