题目内容
已知函数f(x)=2
sin(x-
)cos(x-
)-sin(2x-π).
(1)求f(x)的单调递增区间;
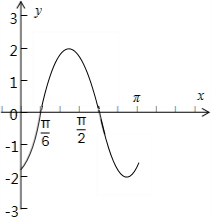
(2)试画出函数f(x)在区间[0,π]上的图象.
| 3 |
| π |
| 4 |
| π |
| 4 |
(1)求f(x)的单调递增区间;
(2)试画出函数f(x)在区间[0,π]上的图象.
(1)函数f(x)=2
sin(x-
)cos(x-
)-sin(2x-π)
=
sin(2x-
)-sin(2x-π)
=sin2x-
cos2x
=2sin(2x-
).
由-
+2kπ≤2x-
≤2kπ+
,k∈Z,
得-
+kπ≤x≤kπ+
,k∈Z,
故函数的单调增区间是[-
+kπ,kπ+
], k∈Z.
(2)函数f(x)=2sin(2x-
).列表如下:
函数的图象为:
| 3 |
| π |
| 4 |
| π |
| 4 |
=
| 3 |
| π |
| 2 |
=sin2x-
| 3 |
=2sin(2x-
| π |
| 3 |
由-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
得-
| π |
| 12 |
| 5π |
| 12 |
故函数的单调增区间是[-
| π |
| 12 |
| 5π |
| 12 |
(2)函数f(x)=2sin(2x-
| π |
| 3 |
| x | 0 |
|
|
|
|
π | ||||||||||
2x-
|
-
|
0 |
|
π |
|
| ||||||||||
| y | -
|
0 | 2 | 0 | -2 | -
|


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目