题目内容
如图,已知四棱锥P—ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点.又BO=2,PO=![]() ,PB⊥PD.
,PB⊥PD.
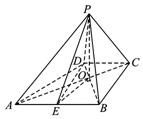
(Ⅰ)求异面直线PD与BD所成角的余弦值;
(Ⅱ)求二面角P—AB—C的大小;
(Ⅲ)设点M在棱PC上,且![]() =λ,问λ为何值时,PC⊥平面BMD.
=λ,问λ为何值时,PC⊥平面BMD.
解法一:
∵PO⊥平面ABCD,∴PO⊥BD.又PB⊥PD,BO=2,PO=![]() ,
,
由平面几何知识得:OD=1,PD=![]() ,PB=
,PB=![]() .
.
(Ⅰ)过D作DE∥BC交于AB于E.连结PE,则∠PDE或其补角为异面直线PD与BC所成的角.

∵四边形ABCD是等腰梯形,
∴OC=OD=1,OB=OA=2,OA⊥OB.
∴BC=![]() ,AB=2
,AB=2![]() ,CD=
,CD=![]()
又AB∥DC,
∴四边形EBCD是平行四边形.
∴ED=BC=![]() ,BE=CD=
,BE=CD=![]() .
.
∴E是AB的中点,且AE=![]() .
.
又PA=PB=![]() ,
,
∴△PEA为直角三角形.
∴PE=![]() =2.
=2.
在△PED中,由余弦定理得
cos∠PDE=![]() .
.
故异面直线PD与BC所成的角的余弦值为![]() .
.
(Ⅱ)连结OE,由(Ⅰ)及三垂线定理知,∠PEO为二面角P—AB—C的平面角.
∴sin∠PEO=![]() =
=![]() ,
,
∴∠PEO=45°.
∴二面角P—AB—C的大小为45°.
(Ⅲ)连结MD,MB,MO,
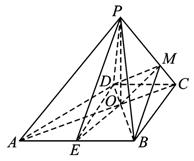
∵PC⊥平面BMD,
OM![]() 平面BMD,
平面BMD,
∴PC⊥OM.
又在Rt△POC中,
PC=PD=![]() ,OC=1,PO=
,OC=1,PO=![]() ,
,
∴PM=![]() ,MC=
,MC=![]() 3,
3,
∴![]() =2.
=2.
故λ=2时,PC⊥平面BMD.
解法二:
∵PO⊥平面ABCD,
∴PO⊥BD.
又PB⊥PD,BO=2,
PO=![]() ,
,
由平面几何知识得
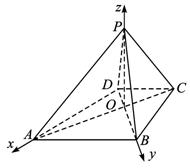
OD=OC=1,BO=AO=2.
以O为原点,OA,OB,OP分别为x,y,z轴建立如图所示的空间直角坐标系,则各点坐标为O(0,0,0),A(2,0,0),B(0,2,0),C(-1,0,0),D(0,-1,0),P(0,0,![]() ).
).
(Ⅰ)![]() =(0,-1,-
=(0,-1,-![]() ),
),![]() =(-1,-2,0),∴|
=(-1,-2,0),∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,
,![]() ·
·![]() =2.
=2.
∴cos〈![]() ,
,![]() 〉=
〉= =
=![]() .
.
故直线PD与BC所成角的余弦值为![]() .
.
(Ⅱ)设平面PAB的一个法向量为n=(x,y,z),由于![]() =(-2,2,0),
=(-2,2,0),![]() =(-2,0,
=(-2,0,![]() ),由
),由
 得
得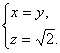
取n=(1,1,![]() ),又平面ABCD的一个法向量m=(0,0,1).
),又平面ABCD的一个法向量m=(0,0,1).
∴cos〈m·n〉=![]() =
=![]() .
.
又二面角P—AB—C为锐二面角,
∴所求二面角P—AB—C的大小为45°.
(Ⅲ)设M(x0,0,z0),由于P、M、C三点线,∴z0=2(x0+1). ①
又PC⊥平面BMD,∴OM⊥PC.即OM·PC=0.∴x0+![]() z0=0. ②
z0=0. ②
由①、②知x0=![]() ,z0=
,z0=![]() ,即M(
,即M(![]() ,0,
,0,![]() ),∴λ=
),∴λ=![]() =2,故λ=2时,PC⊥平面PMD.
=2,故λ=2时,PC⊥平面PMD.

 名校课堂系列答案
名校课堂系列答案 如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点,
如图:已知四棱锥P-ABCD中,PD⊥平面ABCD,ABCD是正方形,E是PA的中点, 如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点. 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=60°,PD⊥AD.点E是BC边上的中点. (2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2.
(2012•崇明县二模)如图,已知四棱锥P-ABCD的底面ABCD为正方形,PA⊥平面ABCD,E、F分别是BC,PC的中点,AB=2,AP=2. (2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,
(2012•吉林二模)如图,已知四棱锥P-ABCD的底面是正方形,PA⊥面ABCD,且PA=AD=2,点M,N分别在PD,PC上,