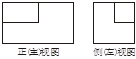题目内容
一个几何体的三视图如图所示,则这个几何体的体积为
A. | B.   | C. | D. |
D
解析试题分析:观察三视图可知,这是一个三棱柱,底面直角三角形直角边长分别为1,2,几何体高为2,所以几何体体积为, ,故选D。
,故选D。
考点:本题主要考查三视图,几何体的体积计算。
点评:基础题,三视图是高考必考题目,因此,要明确三视图视图规则,准确地还原几何体,明确几何体的特征,以便进一步解题。三视图视图过程中,要注意虚线的出现,意味着有被遮掩的棱。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的表面积为( )
A. | B. |
C. | D. |
已知某三棱锥的三视图(单位:Cm)如图所示,则该三棱锥的体积是( )
| A. 6cm3 | B.2cm3 | C.3 cm3 | D.1cm3 |
将一个等腰梯形绕着它的较长的底边所在的直线旋转一周,所得的几何体包括
| A.一个圆台、两个圆锥 | B.两个圆台、一个圆柱 |
| C.两个圆台、一个圆锥 | D.一个圆柱、两个圆锥 |
正方体的内切球和外接球的半径之比为
A. | B. | C. | D. |
某三棱锥的侧视图和俯视图如图所示,则该三棱锥的体积为
A. | B. | C. | D. |