Question

若函数y=cosx（0≤x≤2π）的图象与直线y=1围成一个封闭的平面图形，则这个图形的面积为（　　）

A．

2

B．

4

C．

π

D．

2π

Answer 1

考点：

定积分在求面积中的应用．

分析：

画出函数y=cosx（0≤x≤2π）的图象与直线y=1围成一个封闭的平面图形，作出y=﹣2的图象，容易求出封闭图形的面积．

解答：

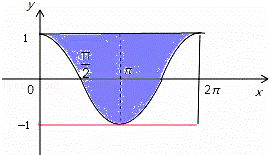
解：画出函数y=cosx（0≤x≤2π）的图象与直线y=1围成一个封闭的平面图形如图：

显然图中封闭图形的面积，

就是矩形面积的一半，=2π．

故选D．

点评：

本题考查余弦函数的图象、几何图形的面积的求法、图象的对称性解答，考查发现问题解决问题的能力．是基础题，