题目内容
一个正三棱柱的主（正）视图是边长为
的正方形，则它的外接球的表面积等于（ ）
A． | B．  |
C．9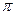 | D． |
B
解析
练习册系列答案
相关题目
的正三棱柱的三视图如图所示，则这个三棱柱的左视图的面积为
，那么它的表面积为___________.
以长方体ABCD—A1B1C1D1的六条面对角线为棱，可以构成四面体A—B1CD1，A1—BC1D，若这两个四面体组合起来的体积为1（重合部分只算一次），则长方体的体积为
（ ）
| A．2 | B． | C．3 | D．4 |
一个棱锥的三视图如右图所示，则它的体积为
A． | B． | C．1 | D． |
如图，体积为V的大球内有4个小球，每个小球的球面过大球球心且与大球球面有且只有一个交点，4个小球的球心是以大球球心为中心的正方形的4个顶点.V1为小球相交部分（图中阴影部分）的体积，V2为大球内、小球外的图中黑色部分的体积，则下列关系中正确的是
A．V1= | B． V2= |
| C．V1> V2 | D．V1< V2 |
下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
| A．9π | B．10π | C．11π | D．12π |