题目内容
已知函数 按向量
按向量 平移后所得函数y=f(x)是奇函数,则
平移后所得函数y=f(x)是奇函数,则 可以是
可以是
- A.

- B.

- C.

- D.

B
分析:设 =(μ,v),可求得函数
=(μ,v),可求得函数 的按向量
的按向量 平移后所得函数的函数解析式,利用正弦函数与余弦函数相互转化的规律即可得到答案.
平移后所得函数的函数解析式,利用正弦函数与余弦函数相互转化的规律即可得到答案.
解答:设 =(μ,v),
=(μ,v),
则函数 的按向量
的按向量 平移后得:
平移后得:
y=f(x)=-3cos[2(x-μ)+ ]+4+v
]+4+v
=-3cos[2x+( -2μ)]+4+v,
-2μ)]+4+v,
∵函数y=f(x)是奇函数,
∴ -2μ=kπ+
-2μ=kπ+ ,4+v=0,
,4+v=0,
∴μ=- -
- ,
,
∴ =(-
=(- -
- ,-4),
,-4),
令k=0,得 =(-
=(- ,-4),即选项B.
,-4),即选项B.
故选B.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,求得按向量 平移后所得函数的函数解析式是关键,余弦函数转化为正弦函数是难点,考查分析问题、转化解决问题的能力,属于中档题.
平移后所得函数的函数解析式是关键,余弦函数转化为正弦函数是难点,考查分析问题、转化解决问题的能力,属于中档题.
分析:设
 =(μ,v),可求得函数
=(μ,v),可求得函数 的按向量
的按向量 平移后所得函数的函数解析式,利用正弦函数与余弦函数相互转化的规律即可得到答案.
平移后所得函数的函数解析式,利用正弦函数与余弦函数相互转化的规律即可得到答案.解答:设
 =(μ,v),
=(μ,v),则函数
 的按向量
的按向量 平移后得:
平移后得:y=f(x)=-3cos[2(x-μ)+
 ]+4+v
]+4+v=-3cos[2x+(
 -2μ)]+4+v,
-2μ)]+4+v,∵函数y=f(x)是奇函数,
∴
 -2μ=kπ+
-2μ=kπ+ ,4+v=0,
,4+v=0,∴μ=-
 -
- ,
,∴
 =(-
=(- -
- ,-4),
,-4),令k=0,得
 =(-
=(- ,-4),即选项B.
,-4),即选项B.故选B.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,求得按向量
 平移后所得函数的函数解析式是关键,余弦函数转化为正弦函数是难点,考查分析问题、转化解决问题的能力,属于中档题.
平移后所得函数的函数解析式是关键,余弦函数转化为正弦函数是难点,考查分析问题、转化解决问题的能力,属于中档题. 
练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
 (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,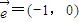 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称. ,下列结论正确的个数为( )
,下列结论正确的个数为( ) 对称
对称 上单调递增
上单调递增 平移后,所得图象关于原点对称.
平移后,所得图象关于原点对称. ,下列结论正确的个数为( )
,下列结论正确的个数为( ) 对称
对称 上单调递增
上单调递增 平移后,所得图象关于原点对称.
平移后,所得图象关于原点对称.