题目内容
若某空间几何体的三视图如图所示,则该几何体的体积是( ) 
| A.2 | B.1 | C. | D. |
B
解析考点:由三视图求面积、体积.
专题:计算题.
分析:三视图,联想几何体是直三棱柱,结合该几何体三视图的数据求出几何体的体积.
解答:解:由该几何体的三视图可知,该几何体是直三棱柱,
且棱柱的底面是两直角边长分别为 和1的直角三角形,
和1的直角三角形,
棱柱的高为 ,
,
所以该几何体的体积V=S底?h=(
 ×1)×
×1)× =1.
=1.
故选B.
点评:本题考查三视图的概念及空间想象能力,注意三视图复原几何体的特征,属中等题.

练习册系列答案
相关题目
在四面体S—ABC中, ,二面角S—AC—B的余弦值是
,二面角S—AC—B的余弦值是 ,则该四面体外接球的表面积是 (
,则该四面体外接球的表面积是 (  )
)
A. | B. | C.24 | D.6 |
已知正方体外接球的体积是 ,那么正方体的棱长等于 ( )
,那么正方体的棱长等于 ( )
A. | B. | C. | D. |
如图为一个几何体的三视图,左视图和主视图均为矩形,俯视图为正三角形,尺寸如图,则该几何体的全面积为
A. | B.12 | C.24 | D. |
一梯形直观图是一个如图所示的等腰梯形,且梯形OA/B/C/面积 ,则原梯形面积为
,则原梯形面积为
| A.2 | B. | C.2 | D. 4 |
 的正方形
的正方形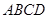 沿对角线
沿对角线 折起,使得平面
折起,使得平面 平面
平面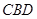 ,形成三棱锥
,形成三棱锥 的正视图与俯视图如右图所示,则侧视图的面积为
的正视图与俯视图如右图所示,则侧视图的面积为












 是球
是球 表面上的点,
表面上的点, ,
, ,
, ,
, ,则球
,则球
