题目内容
已知一个圆台的下底面半径为r，高为h，当圆台的上底半径r′变化时，圆台体积的变化范围是
（
πr2h，+∞）
| 1 |
| 3 |
（
πr2h，+∞）
．| 1 |
| 3 |
分析：根据圆台的体积公式，分析求解．
解答：解：V圆台=
π（r2+rr′+r′2）h．
∵r′＞0，∴当上底面积为0时，V圆锥=
πr2h，
随上底半径的增大，V圆台增大．
∴V圆台＞
πr2h，
故答案是（
πr2h，+∞）．
| 1 |
| 3 |
∵r′＞0，∴当上底面积为0时，V圆锥=
| 1 |
| 3 |
随上底半径的增大，V圆台增大．
∴V圆台＞
| 1 |
| 3 |
故答案是（
| 1 |
| 3 |
点评：本题考查圆台的体积公式．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
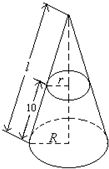把一个圆锥截成圆台，已知圆台的上、下底面半径的比是1：4，母线长10cm．求：圆锥的母线长．