题目内容
在椭圆中,我们有如下结论:椭圆
+
=1上斜率为1的弦的中点在直线
+
=0上,类比上述结论,得到正确的结论为:双曲线
-
=1上斜率为1的弦的中点在直线______上.
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| a2 |
| y |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆
+
=1上斜率为1的弦的中点在直线
+
=0上,
观察所得的直线方程与椭圆的方程之间的关系,直线的方程有两个变化,
即x,y的平方变化成x,y,等号右边的1变成0,
∴双曲线
-
=1上斜率为1的弦的中点在直线
-
=0上,
故答案为:
-
=0
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| a2 |
| y |
| b2 |
观察所得的直线方程与椭圆的方程之间的关系,直线的方程有两个变化,
即x,y的平方变化成x,y,等号右边的1变成0,
∴双曲线
| x2 |
| a2 |
| y2 |
| b2 |
| x |
| a2 |
| y |
| b2 |
故答案为:
| x |
| a2 |
| y |
| b2 |

练习册系列答案
相关题目
 上斜率为1的弦的中点在直线
上斜率为1的弦的中点在直线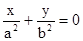 上,类比上述结论,得到正确的结论为:双曲线
上,类比上述结论,得到正确的结论为:双曲线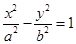 上斜率为1的弦的中点在直线
上
上斜率为1的弦的中点在直线
上 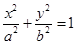 上斜率为1的弦的中点在直线
上斜率为1的弦的中点在直线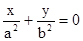 上,类比上述结论,得到正确的结论为:双曲线
上,类比上述结论,得到正确的结论为:双曲线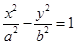 上斜率为1的弦的中点在直线 上.
上斜率为1的弦的中点在直线 上.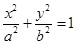 上斜率为1的弦的中点在直线
上斜率为1的弦的中点在直线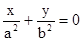 上,类比上述结论,得到正确的结论为:双曲线
上,类比上述结论,得到正确的结论为:双曲线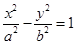 上斜率为1的弦的中点在直线
上.
上斜率为1的弦的中点在直线
上.