题目内容
【题目】【2018福建福州市一中高三上学期期中考试】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,点
,点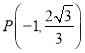 在椭圆上,且
在椭圆上,且![]() 与
与![]() 轴交点恰为
轴交点恰为![]() 中点.
中点.
(I)求椭圆![]() 的方程;
的方程;
(II)过![]() 作两条互相垂直的直线,分别交椭圆
作两条互相垂直的直线,分别交椭圆![]() 于点
于点![]() 和
和![]() .求四边形
.求四边形![]() 的面积的最小值.
的面积的最小值.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】试题分析:(1)由题意易得![]() ,即
,即![]() ,根据椭圆的定义
,根据椭圆的定义![]() 可求出
可求出![]() 的值,故而可求出
的值,故而可求出![]() ,即可求出椭圆的方程;(2)考虑直线
,即可求出椭圆的方程;(2)考虑直线![]() 的斜率为0或不存在,分别求得面积,讨论当直线
的斜率为0或不存在,分别求得面积,讨论当直线![]() 的斜率存在且不为零时,设直线
的斜率存在且不为零时,设直线![]() 的方程为
的方程为![]() ,(
,( ![]() ),代入椭圆方程,运用韦达定理和弦长公式可得
),代入椭圆方程,运用韦达定理和弦长公式可得![]() ,将
,将![]() 换为
换为![]() 得
得![]() ,由四边形的面积公式,运用换元法和基本不等式,可得最小值;,即可得到面积的最小值
,由四边形的面积公式,运用换元法和基本不等式,可得最小值;,即可得到面积的最小值
试题解析:(1)依题意, ![]() ,另一焦点坐标为
,另一焦点坐标为![]() ,
,
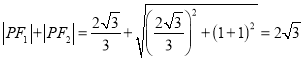 ,所以
,所以![]() ,
, ![]() ,所以
,所以![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)当![]() 垂直于坐标轴时,
垂直于坐标轴时, ![]() ,
, ![]() ,
, ![]() ,
,
当![]() 不垂直于坐标轴时,设直线
不垂直于坐标轴时,设直线![]() 的方程为
的方程为![]() ,
, ![]() ,
, ![]() ,
, ![]()
由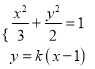 ,得
,得![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
,
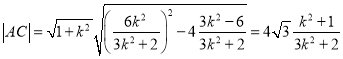 ,
,
同理, 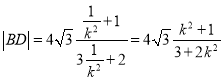 ,
,
所以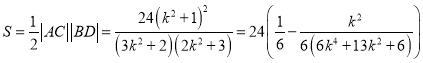 ,
,
因为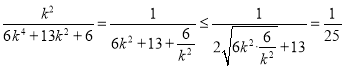 ,当且仅当
,当且仅当![]() ,即
,即![]() 时等号成立,所以
时等号成立,所以![]() .
.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目