题目内容
已知空间向量a＝(1，n,2)，b＝(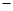
2,1,2)，若2a-b与b垂直，则|a|等于 ( )
A． | B． | C． | D． |
D
解析试题分析：2a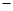b=(4，2n-1,2)，由于2a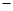b与b垂直，所以（2a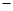b）·b=-8+2n-1+4=0,得n=
，所以|a|=
考点：1.空间中的点的坐标运算与模；2.向量的数量积判断向量的共线与垂直．
练习册系列答案
相关题目
若
，
，且
，则
与
的夹角是（ ）
A． | B． | C． | D． |
角
顶点在坐标原点
，始边与
轴的非负半轴重合，
，点
在的终边上，点
，则
与
夹角余弦值为( )
A． | B． | C． 或 | D．或 |
已知向量
，
，且
，则
等于（ ）
A． | B． |
C． | D． |
已知向量
、
满足
，
，且
，则与的夹角为（ ）
A． | B． | C． | D． |
已知向量
,
,
,若
为实数，
，则的值为（ ）
A． | B． | C． | D． |
已知
为单位向量，当
的夹角为
时，
在
上的投影为（ ）
| A．5 | B． | C． | D． |
已知长方体
，下列向量的数量积一定不为
的是（ ）
A． | B． | C． | D． |
若向量
与
不共线，
，且
，则向量与
的夹角为 ( )
| A．0 |
B． |
C． |
D． |