题目内容
等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，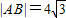
，则C的实轴长为（ ）A．
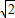
B．
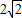
C．4
D．8
【答案】分析：设等轴双曲线C：x2-y2=a2（a＞0），y2=16x的准线l：x=-4，由C与抛物线y2=16x的准线交于A，B两点，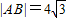
，能求出C的实轴长．
解答：解：设等轴双曲线C：x2-y2=a2（a＞0），
y2=16x的准线l：x=-4，
∵C与抛物线y2=16x的准线l：x=-4交于A，B两点，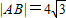
∴A（-4，2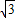
），B（-4，-2
），
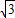将A点坐标代入双曲线方程得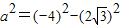
=4，
∴a=2，2a=4．
故选C．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答，注意挖掘题设中的隐含条件，合理地进行等价转化．
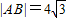，能求出C的实轴长．解答：解：设等轴双曲线C：x2-y2=a2（a＞0），
y2=16x的准线l：x=-4，
∵C与抛物线y2=16x的准线l：x=-4交于A，B两点，
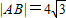
∴A（-4，2
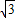），B（-4，-2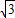），将A点坐标代入双曲线方程得
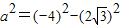=4，∴a=2，2a=4．
故选C．
点评：本题考查双曲线的性质和应用，解题时要认真审题，仔细解答，注意挖掘题设中的隐含条件，合理地进行等价转化．
练习册系列答案
相关题目