Question

如图,圆x²+y²=r²的弦AB垂直于x轴,P为AB上一点,且|AP|·|PB|=a²(a≤r)为定值,求点P的轨迹方程.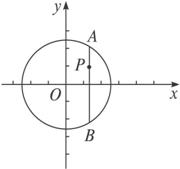

Answer 1

解:设A(rcosφ,rsinφ),则点B(rcosφ,-rsinφ),P(x,y).

∵AB⊥x轴,∴x=rcosφ,|AP|=|rsinφ-y|,|PB|=|y+rsinφ|.

∵|AP|·|PB|=|(rsinφ-y)·(rsinφ+y)|=a²|y²-r²sin²φ|=a²,

∵|y|≤|rsinφ|,∴r²sin²φ-y²=a².

∴y²+a²=r²sin²φ.又x=rcosφ,

∴x²+y²+a²=r²x²+y²=r²-a².