已知圆C:x2+y2+4x-12y+39=0和一条直线l:3x-4y+5=0,求圆C关于直线l对称的圆的方程. 题目和参考答案——青夏教育精英家教网——

题目内容

已知圆C:x²+y²+4x-12y+39=0和一条直线l:3x-4y+5=0,求圆C关于直线l对称的圆的方程.

思路解析：由于圆关于直线对称的圆的大小不变,即半径不变,而只有圆心变化,所以只需根据条件求出圆心关于直线的对称点即可.

解：因为圆C的方程可化为(x+2)²+(y-6)²=1,所以圆心为C(-2,6),半径为1,设所求圆的圆心为D(a,b),则点C、D关于直线l对称,

所以解之,得

故所求圆的方程为(x-4)²+(y+2)²=1.

练习册系列答案

师说系列答案

实验班培优训练系列答案

数理报系列答案

培优竞赛新方法系列答案

素养提升讲练系列答案

数学指导系列答案

导学与训练系列答案

导与学学案导学系列答案

地道中考系列答案

地理图册系列答案

相关题目

已知圆C:x²+y²-4x-14y+45=0及点Q(-2,3).?

(1)若点P(m,m+1)在圆C上，求直线PQ的斜率；?

(2)若M是圆上任一点，求|MQ|的最大值和最小值；

(3)若点N（a,b）满足关系式a²+b²-4a-14b+45=0，求的最大值.

已知圆C:x²+y²+2x-4y+3=0.

(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;

(2)从圆C外一点P(x₁,y₁)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值的点P的坐标.

(理)已知圆C:x²+y²-4x-2y+1=0,直线l:3x-4y+k=0,圆上存在两点到直线l的距离为1,则k的?取值范围是

A.(-17,-7) B.(3,13)

C.(-17,-7)∪(3,13) D.［-17,-7］∪［3,13］

已知圆C:x²+y²-2x+4y=0，则过原点且与圆C相切的直线方程为

A.y=-2x B.y=x

C.y=x D.y=2x

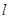已知圆C:x²+y²+2x+ay-3=0(a为实数)上任意一点关于直线：x-y+2=0的对称点都在圆C上，则a= .