Question

如图,在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2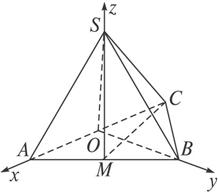,M为AB的中点.

(1)证明：AC⊥SB;

(2)求二面角S—CM—A的大小;

(3)求点B到平面SCM的距离.

Answer 1

答案：（1）证明：取AC中点O，连结OS、OB.

因为SA=SC,BA=BC,所以AC⊥SO且AC⊥BO.

因为平面SAC⊥平面ABC,平面SAC∩平面ABC=AC,

所以SO⊥面ABC.所以SO⊥BO.

如图所示,建立空间直角坐标系O—xyz,

则A(2,0,0),C(-2,0,0),S(0,0,2),B(0,2,0).

所以=（-4，0，0），=（0，-2，2）.

因为·=(-4,0,0)·(0,-2,2)=0,

所以AC⊥BS.

(2)解:由(1)得M(1,,0).

所以=(3,,0),=(2,0,2).

设n=(x,y,z)为平面SCM的一个法向量,

则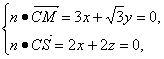

取z=1,则x=-1,y=,所以n=(-1,,1).

又=(0,0,2)为平面ABC的一个法向量，

所以cos〈n,〉=.

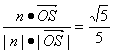所以二面角S—CM—A的大小为arccos.

(3)解：由（1）（2），得=（2，2，0），n=(-1,,1)为平面SCM的一个法向量，

所以点B到平面SCM的距离d=.