题目内容
已知函数f(x)=lnx-ax+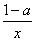 -1(a∈R),
-1(a∈R),
(Ⅰ)当a≤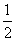 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;
(Ⅱ)设g(x)=x2-2bx+4,当a=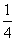 时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b的取值范围。
时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b的取值范围。
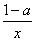 -1(a∈R),
-1(a∈R),(Ⅰ)当a≤
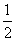 时,讨论f(x)的单调性;
时,讨论f(x)的单调性;(Ⅱ)设g(x)=x2-2bx+4,当a=
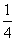 时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b的取值范围。
时,若对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2),求实数b的取值范围。 解:(Ⅰ)因为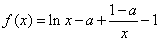 ,
,
所以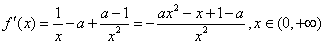 ,
,
令h(x)=ax2-x+1-a,x∈(0,+∞),
①当a=0时,h(x)=-x+1,x∈(0,+∞),
所以当x∈(0,1)时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;
②当a≠0时,由f′(x)=0,即ax2-x+1-a=0,解得x1=1,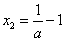 ,
,
(ⅰ)当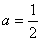 时,x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
时,x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
(ⅱ)当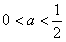 时,
时,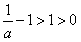 ,x∈(0,1)时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
,x∈(0,1)时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
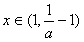 时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;
时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;
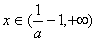 时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
(ⅲ)当a<0时,由于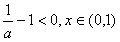 时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
x∈(1,+∞)时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;
综上所述,当a≤0时,函数f(x)在(0,1)上单调递减,函数f(x)在(1,+∞)上单调递增;
当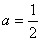 时,函数f(x)在(0,+∞)上单调递减;
时,函数f(x)在(0,+∞)上单调递减;
当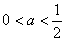 时,函数f(x)在(0,1)上单调递减,函数f(x)在
时,函数f(x)在(0,1)上单调递减,函数f(x)在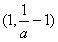 上单调递增,
上单调递增,
函数f(x)在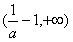 上单调递减;
上单调递减;
(Ⅱ)因为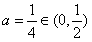 ,由(Ⅰ)知,x1=1,x2=3
,由(Ⅰ)知,x1=1,x2=3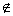 (0,2),
(0,2),
当x∈(0,1)时,f′(x)<0,函数f(x)单调递减;
当x∈(1,2)时,f′(x)>0,函数f(x)单调递增,所以f(x)在(0,2)上的最小值为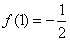 ,
,
由于“对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2)” 等价于“g(x)在[1,2]上的最小值不大于f(x)在(0,2)上的最小值”,
又g(x)=(x-b)2+4-b2,x∈[1,2],
所以(ⅰ)当b<1时,因为[g(x)]min=g(1)=5-2b>0,此时与(*)矛盾;
(ⅱ)当b∈[1,2]时,因为[g(x)]min=4-b2≥0,同样与(*)矛盾;
③当b∈(2,+∞)时,因为[g(x)]min=g(2)=8-4b,
解不等式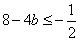 ,可得
,可得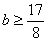 ;
;
综上,b的取值范围是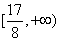 。
。
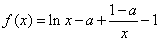 ,
,所以
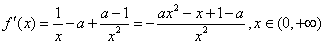 ,
,令h(x)=ax2-x+1-a,x∈(0,+∞),
①当a=0时,h(x)=-x+1,x∈(0,+∞),
所以当x∈(0,1)时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
当x∈(1,+∞)时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;
②当a≠0时,由f′(x)=0,即ax2-x+1-a=0,解得x1=1,
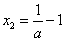 ,
,(ⅰ)当
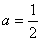 时,x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)上单调递减;
时,x1=x2,h(x)≥0恒成立,此时f′(x)≤0,函数f(x)在(0,+∞)上单调递减;(ⅱ)当
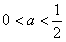 时,
时,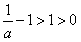 ,x∈(0,1)时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
,x∈(0,1)时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;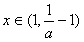 时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;
时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;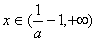 时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;(ⅲ)当a<0时,由于
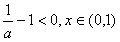 时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;
时,h(x)>0,此时f′(x)<0,函数f(x)单调递减;x∈(1,+∞)时,h(x)<0,此时f′(x)>0,函数f(x)单调递增;
综上所述,当a≤0时,函数f(x)在(0,1)上单调递减,函数f(x)在(1,+∞)上单调递增;
当
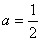 时,函数f(x)在(0,+∞)上单调递减;
时,函数f(x)在(0,+∞)上单调递减;当
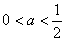 时,函数f(x)在(0,1)上单调递减,函数f(x)在
时,函数f(x)在(0,1)上单调递减,函数f(x)在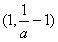 上单调递增,
上单调递增,函数f(x)在
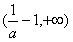 上单调递减;
上单调递减;(Ⅱ)因为
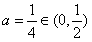 ,由(Ⅰ)知,x1=1,x2=3
,由(Ⅰ)知,x1=1,x2=3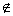 (0,2),
(0,2),当x∈(0,1)时,f′(x)<0,函数f(x)单调递减;
当x∈(1,2)时,f′(x)>0,函数f(x)单调递增,所以f(x)在(0,2)上的最小值为
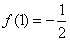 ,
,由于“对任意x1∈(0,2),存在x2∈[1,2],使f(x1)≥g(x2)” 等价于“g(x)在[1,2]上的最小值不大于f(x)在(0,2)上的最小值”,
又g(x)=(x-b)2+4-b2,x∈[1,2],
所以(ⅰ)当b<1时,因为[g(x)]min=g(1)=5-2b>0,此时与(*)矛盾;
(ⅱ)当b∈[1,2]时,因为[g(x)]min=4-b2≥0,同样与(*)矛盾;
③当b∈(2,+∞)时,因为[g(x)]min=g(2)=8-4b,
解不等式
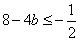 ,可得
,可得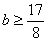 ;
;综上,b的取值范围是
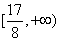 。
。 
练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目