题目内容
【题目】已知椭圆![]() 过点
过点![]() 且椭圆的短轴长为
且椭圆的短轴长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知动直线![]() 过右焦点
过右焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得,
,使得,![]() 恒成立?若存在求出点
恒成立?若存在求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)存在,
(Ⅱ)存在,![]()
【解析】
(Ⅰ)由椭圆性质可知![]() ,点代入即可求得结果.
,点代入即可求得结果.
(Ⅱ)假设存在定点![]() 符合题意,①当直线
符合题意,①当直线![]() 的斜率不存在时,由
的斜率不存在时,由![]() 解得
解得![]() 或
或![]() ;②当直线
;②当直线![]() 的斜率为0时,解得
的斜率为0时,解得![]() 或
或![]() .由①②可得
.由①②可得![]() ,然后证明当
,然后证明当![]() 时,通过方程联立,借助韦达定理,坐标表示
时,通过方程联立,借助韦达定理,坐标表示![]() 即可证得结论.
即可证得结论.
解:(Ⅰ)因为椭圆![]() 过点
过点![]() ,所以
,所以![]() .
.
又椭圆的短轴长为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
解得![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)假设在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() ,
,
①当直线![]() 的斜率不存在时,则
的斜率不存在时,则![]() ,
,![]() ,
,
![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() ;
;
②当直线![]() 的斜率为0时,则
的斜率为0时,则![]() ,
,![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() .
.
由①②可得![]() ,即点
,即点![]() 的坐标为
的坐标为![]() .
.
下面证明当![]() 时,
时,![]() 恒成立,当直线
恒成立,当直线![]() 的斜率不存在或斜率为0时,由①②知结论成立.
的斜率不存在或斜率为0时,由①②知结论成立.
当直线斜率存在且不为0时,设其方程为![]() ,
,![]() ,
,![]() ,
,
由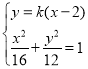 ,得
,得![]() ,
,
直线经过椭圆内一点,一定与椭圆有两个交点,
且![]() ,
,![]() .
.
![]() ,
,
所以![]()
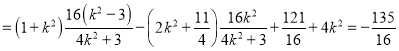 .
.
综上所述,在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 恒成立..
恒成立..

【题目】某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 40 | 20 | 20 | 20 |
乙分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 28 | 17 | 34 | 21 |
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
【题目】(理)某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定:![]() 三级为合格等级,
三级为合格等级,![]() 为不合格等级.
为不合格等级.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
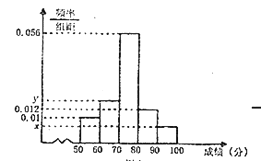
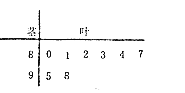
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选3人,求至少有1人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 两个等级的学生中随机抽取了3名学生进行调研,记
两个等级的学生中随机抽取了3名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
