题目内容
在△ABC中，cosA=-
，cosB=
，BC=5，△ABC的面积=______．
| 5 |
| 13 |
| 3 |
| 5 |
∵cosA=-
，cosB=
，
∴sinA=
=
，sinB=
=
，
∴sinC=sin（A+B）=sinAcosB+cosAsinB=
×
-
×
=
，
∵BC=a=5，
∴由正弦定理
=
得：c=
=
，
则S△ABC=
acsinB=
×5×
×
=
．
故答案为：
| 5 |
| 13 |
| 3 |
| 5 |
∴sinA=
| 1-cos2A |
| 12 |
| 13 |
| 1-cos2B |
| 4 |
| 5 |
∴sinC=sin（A+B）=sinAcosB+cosAsinB=
| 12 |
| 13 |
| 3 |
| 5 |
| 5 |
| 13 |
| 4 |
| 5 |
| 16 |
| 65 |
∵BC=a=5，
∴由正弦定理
| a |
| sinA |
| c |
| sinC |
| asinC |
| sinA |
| 4 |
| 3 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 4 |
| 5 |
| 8 |
| 3 |
故答案为：
| 8 |
| 3 |
练习册系列答案
计算高手系列答案
相关题目
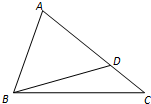如图，在△ABC中，cos∠ABC=