Question

【题目】已知椭圆过点，且左焦点与抛物线的焦点重合。

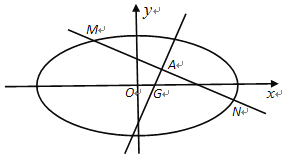
（1）求椭圆的标准方程；

（2）若直线与椭圆交于不同的两点、，线段的中点记为，且线段的垂直平分线过定点，求的取值范围。

Answer 1

【答案】(1) (2)

【解析】

（1）由左焦点与抛物线的焦点重合，可以求得c,再利用椭圆过点求得、，从而求出椭圆方程。

（2）由直线与椭圆交于不同的两点，可以由 得到k与m的不等关系，再由AG直线与直线垂直，斜率乘积为-1，得到k与m的等量关系，将等量关系代入不等关系来限定k的取值范围。

（1）〖解法1〗抛物线的焦点为F（-1,0），

依题意知，椭圆的左右焦点坐标分别为，

又椭圆过点，∴由椭圆的定义知，，

∴，又，∴

∴椭圆的方程为．

（1）〖解法2〗抛物线的焦点为F（-1,0），

依题意知，椭圆的左右焦点坐标分别为，

又椭圆过点，∴

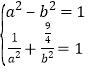
解得，

∴椭圆的方程为．

（1）〖解法3〗抛物线的焦点为F（-1,0），

依题意知，椭圆的左右焦点坐标分别为，

又椭圆过点，∴

∴，∵

∴可解得，

∴椭圆的方程为．

（2）〖解法1〗由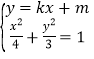消去整理得

，

直线与椭圆交于不同的两点，

，整理得……①

设，线段的中点A，

则，

∴∴，

∴点A的坐标为，

∴直线AG的斜率为，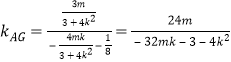

又直线AG和直线MN垂直，

∴，∴，

将上式代入①式，可得，

整理得，解得．

∴实数的取值范围为．

（2）〖解法2〗设

则 两式相减得

即

点满足方程 ①.

又直线且过点

点也满足方程 ②

联立①②解得，即

点在椭圆内部

的取值范围为