题目内容
甲、乙两人同时参加奥运志愿者的选拔赛，已知在备选的10道题中，甲能答对其中的6题，乙能答对其中的8题，规定每次考试都从备选题中随机抽出3题进行测试，至少答对2题才能入选．
（1）求甲答对试题数
的分布列及数学期望；
（2）求甲、乙两人至少有一人入选的概率．
（1）求甲答对试题数
的分布列及数学期望；（2）求甲、乙两人至少有一人入选的概率．
（1）
（2）甲、乙两人于少有一人考试合格的概率为
（2）甲、乙两人于少有一人考试合格的概率为
解：（1）依题意，甲答对主式题数的可能取值为0,1,2,3，则
4分
的分布列为
甲答对试题数的数学期望为
6分
（2）设甲、乙两人考试合格的事件分别为A、B，则
9分
因为事件A、B相互独立，
甲、乙两人考试均不合格的概率为
甲、乙两人至少有一人考试合格的概率为
答：甲、乙两人于少有一人考试合格的概率为 12分
另解：甲、乙两人至少有一个考试合格的概率为
答：甲、乙两人于少有一人考试合格的概率为
的可能取值为0,1,2,3，则 4分的分布列为| | 0 | 1 | 2 | 3 |
| P |  |  |  |  |
的数学期望为 6分（2）设甲、乙两人考试合格的事件分别为A、B，则
9分因为事件A、B相互独立，
甲、乙两人考试均不合格的概率为甲、乙两人至少有一人考试合格的概率为答：甲、乙两人于少有一人考试合格的概率为
12分另解：甲、乙两人至少有一个考试合格的概率为
答：甲、乙两人于少有一人考试合格的概率为
练习册系列答案
相关题目
。第二、第三门课程取得优秀成绩的概率均为
，且不同课程是否取得优秀成绩相互独立。
)= P(ξ
)，则c ="( " )（ C ）
上海世博会大力倡导绿色出行，并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量，某游客计划在游园期间种植n棵树，已知每棵树是否成活互不影响，成活率都为
，用
表示他所种植的树中成活的棵数，
，试求n与p的值并写出
，一旦发生，将造成某公司300万元的损失.现有甲、乙两种相互独立的预防措施可供选择，单独采用甲、乙预防措施所需的费用分别为40万元和20万元，采用相应预防措施后此突发事件不发生的概率分别为
和
.若预防方案允许甲、乙两种预防措施单独采用、同时采用或都不采用，请分别计算这几种预防方案的总费用，并指出哪一种预防方案总费用最少.
服从正态分布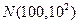
. 已知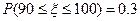
，估计该班数学成绩在110分以上的人数为______________.
表示摸出2个小球的标号之和，写出
．
的概
率分布为右表所示，则
的值为 。