题目内容
13.已知偶函数f(x)的定义域为R,且f(x-1)是奇函数,则下面结论一定成立的是( )| A. | f(x+1)是偶函数 | B. | f(x+1)是非奇非偶函数 | ||
| C. | f(x)=f(x+2) | D. | f(x+3)是奇函数 |
分析 求出周期为4,f(-x+3)=f(-x-1),f(x+3)=-f(x+1)=-f(-x-1),即可得出结论.
解答 解:由题意,f(-x-1)=-f(x-1),∴f(x-2)=-f(-x)=-f(x),∴f(x+2)=-f(x),
∴f(x+4)=f(x),∴函数的周期为4.
∴f(-x+3)=f(-x-1),f(x+3)=-f(x+1)=-f(-x-1),
∴f(-x+3)=-f(x+3),
∴f(x+3)是奇函数,
故选D.
点评 本题考查函数的奇偶性,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
8.执行如图程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=( )


| A. | 7 | B. | 12 | C. | 17 | D. | 34 |
5.已知c>1,则不等式${x}^{2}-(c+\frac{1}{c})x+1>0$的解集为( )
| A. | $\left\{x|\frac{1}{c}<x<c\right\}$ | B. | $\left\{x|x>\frac{1}{c},或x>c\right\}$ | C. | $\left\{x|x<\frac{1}{c},或x>c\right\}$ | D. | $\left\{x|c<x<\frac{1}{c}\right\}$ |
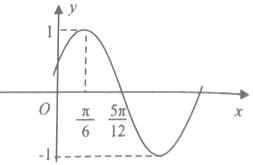 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,