题目内容
11.设等差数列{an}的前n项和为Sn,公差为正整数d.若S32+a32=1,则d的值为1.分析 由题意可得关于a1的一元二次方程,由△≥0和d为正整数可得.
解答 解:∵S32+a32=1,
∴$(3{a}_{1}+3d)^{2}+({a}_{1}+2d)^{2}=1$,
整理可得10${{a}_{1}}^{2}$+22a1d+13d2-1=0,
由关于a1的一元二次方程有实根可得△=(22d)2-40(13d2-1)≥0,
化简可得d2≤$\frac{10}{9}$,由d为正整数可得d=1
故答案为:1
点评 本考查等差数列的通项公式和求和公式,涉及一元二次方程根的存在性,属基础题.

练习册系列答案
相关题目
4.双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的渐近线方程为$y=±\frac{{\sqrt{3}}}{2}x$,则C的离心率为( )
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{7}}}{2}$ | C. | $\sqrt{7}$ | D. | $\frac{{\sqrt{21}}}{3}$ |
16. 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
 如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
如图,在棱长为a的正方体ABCD-A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )| A. | 点P到平面QEF的距离 | B. | 三棱锥P-QEF的体积 | ||
| C. | 直线PQ与平面PEF所成的角 | D. | 二面角P-EF-Q的大小 |
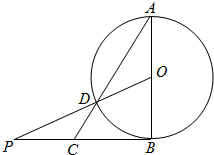 如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$.
如图,AB为圆O的直径,O为圆心,PB与圆O相切于点B,PO交圆O于点D,AD的延长线交PB于点C,若AB=2,$PB=2\sqrt{2}$,则BC=$\sqrt{2}$. 中,
中, ,过
,过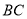 的中点
的中点 作平面
作平面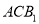 的垂线,交平面
的垂线,交平面 于
于 ,则
,则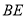 与平面
与平面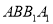 所成角的正切值为( )
所成角的正切值为( )
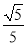 B.
B.
 D.
D.