题目内容
(本题满分15分)
在等比数列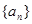 中,
中,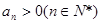 ,公比
,公比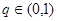 ,且
,且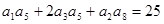 ,
,
又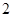 是
是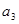 与
与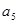 的等比中项。设
的等比中项。设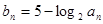 .
.
(Ⅰ) 求数列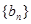 的通项公式;
的通项公式;
(Ⅱ) 已知数列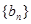 的前
的前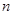 项和为
项和为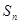 ,
,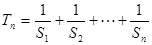 ,求
,求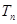 .
.
在等比数列
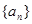 中,
中,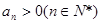 ,公比
,公比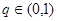 ,且
,且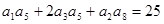 ,
,又
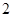 是
是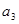 与
与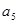 的等比中项。设
的等比中项。设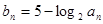 .
.(Ⅰ) 求数列
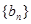 的通项公式;
的通项公式;(Ⅱ) 已知数列
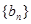 的前
的前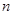 项和为
项和为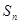 ,
,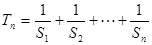 ,求
,求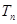 .
. 解:(1) ,
, ,
,
(2)
 。
。
 ,
, ,
,(2)

 。
。本试题主要是考查而来等比数列的性质和裂项求和的综合运用。
(1)根据等比数列中几项的关系式,化简得到公比和首项的值,得到其通项公式。
(2)在第一问的基础上,由 裂项求和得到结论。
裂项求和得到结论。
解:(1) ,
, ,
,
又
 又
又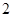 为
为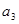 与
与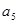 的等比中项,
的等比中项,
而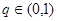 ,
,
 ,
,
 ……………… 5分
……………… 5分
 ………………8分
………………8分
 ………………10分
………………10分
(2)又

 ………15分
………15分
(1)根据等比数列中几项的关系式,化简得到公比和首项的值,得到其通项公式。
(2)在第一问的基础上,由
 裂项求和得到结论。
裂项求和得到结论。解:(1)
 ,
, ,
,又

 又
又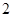 为
为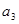 与
与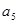 的等比中项,
的等比中项,
而
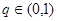 ,
,
 ,
, ……………… 5分
……………… 5分 ………………8分
………………8分 ………………10分
………………10分 (2)又


 ………15分
………15分
练习册系列答案
相关题目
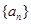 中,
中,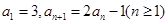
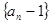 是等比数列;
是等比数列;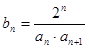 ,求证:数列
,求证:数列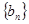 的前
的前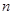 项和
项和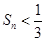 .
.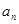 与
与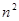 的大小(
的大小(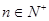 )。
)。 中,
中, 则
则 = ( )
= ( )



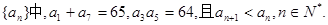
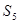 ;
;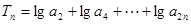 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值. 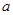 ,
,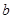 ,
,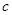 成等比数列,其公比为3,如果
成等比数列,其公比为3,如果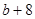 ,
, 成等差数列,求这三个数.
成等差数列,求这三个数. 为等比数列,且
为等比数列,且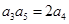 ,设等差数列
,设等差数列 的前
的前 项和为
项和为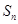 ,若
,若 ,则
,则
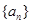 中,
中,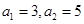 ,其前
,其前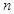 项和
项和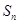 满足:
满足: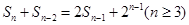 ,令
,令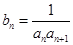 .
.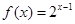 ,求证:
,求证: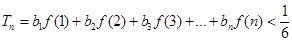 ;
;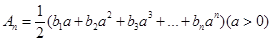 ,问是否存在正实数
,问是否存在正实数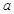 同时满足下列两个条件?
同时满足下列两个条件?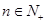 ,都有
,都有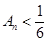 ;
;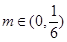 ,均存在
,均存在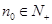 ,使得当
,使得当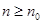 时总有
时总有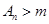 .
. 满足:
满足: 且
且 ,则
,则 _______________.
_______________.  中,
中, ,则
,则 =( )
=( )


