Question

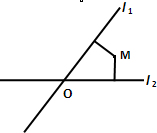
(如图)直线l₁和l₂相交于点M，l₁⊥l₂，点N∈l₁，以A，B为端点的曲线段C上的任一点到l₂的距离与到点N的距离相等，若△AMN为锐角三角形，|AM|＝，|AN|＝3，且|BN|＝6，建立适当的坐标系。求曲线C的方程。

 

Answer 1

答案：
解析：

如图所示建立坐标系，以l1为x轴，MN的垂直平分线为y，轴，点O为坐标原点。     依题意知：曲线段C是以点N为焦点，以l2为准线的抛物线的一段，其中A，B分别为C的端点。     设曲线段C的方程为     y2＝2px(p＞0)，(xA≤x≤xB，y＞0)。     其中xA，xB分别为A，B的横坐标，p＝|MN|     所以     由|AM|=，|AN|=3得     　　　　　　　　　　　　　　　　　　　　  ①     　　　　　　　　　　　　　　　　　　　　  ②         由①、②两式联立解得，再将其代入①式并由P＞0解得     因为△AMN是锐角三角形，所以＞     ∴，由点B在曲线段C上，得，     综上得曲线段C的方程为≤x≤4，y＞0)。