题目内容
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,
,![]() 为椭圆C上一点,且
为椭圆C上一点,且![]() 的中点B在y轴上,
的中点B在y轴上,![]() .
.
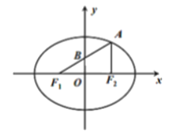
(1)求椭圆C的标准方程:
(2)若直线![]()
![]() 交椭圆于P、Q两点,若PQ的中点为N,O为原点,直线ON交直线
交椭圆于P、Q两点,若PQ的中点为N,O为原点,直线ON交直线![]() 于点M,求
于点M,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由BO为![]() 的中位线,可求出
的中位线,可求出![]() ,由此可设
,由此可设 ,代入椭圆方程,联立
,代入椭圆方程,联立![]() ,
,![]() ,即可求出
,即可求出![]() ,
,![]() ,从而得到椭圆方程;
,从而得到椭圆方程;
(2)设![]() 、
、![]() ,联立
,联立 ,化为关于x的一元二次方程,由根与系数的关系及中点坐标公式求出PQ的中点N的坐标,再由弦长公式求出
,化为关于x的一元二次方程,由根与系数的关系及中点坐标公式求出PQ的中点N的坐标,再由弦长公式求出![]() ,由点N的坐标写出直线ON的方程,求出点M.的坐标,再由两点间距离公式求出
,由点N的坐标写出直线ON的方程,求出点M.的坐标,再由两点间距离公式求出![]() ,然后求
,然后求![]() ,换元法求出其最大值.
,换元法求出其最大值.
(1)因为B为![]() 的中点, O为线段
的中点, O为线段![]() 的中点,
的中点,
所以BO为![]() 的中位线,所以
的中位线,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,所以可设
,所以可设
又![]() 为椭圆C上一点,所以将
为椭圆C上一点,所以将 代入椭圆方程可得
代入椭圆方程可得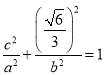
又![]() ,
,![]() ,联立解得
,联立解得![]() ,
,![]() ,
,
故所求椭圆方程为![]() ;
;
(2)由直线方程为![]() ,
,
联立 ,可得
,可得![]() .
.
设![]() 、
、![]() ,则
,则![]() ,
,![]() ,
,
所以为![]()
![]() ;
;
所以PQ的中点N坐标为 ,
,![]()
因此直线ON的方程为![]() ,
,
从而点M为![]() ,又
,又![]() ,所以
,所以![]() ,
,
设
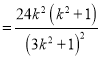 ,令
,令![]() ,则
,则![]() ,
,
所以![]()
![]()
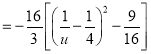 ,
,
因此当![]() ,即
,即![]() 时
时![]() 取得最大值
取得最大值![]() .
.

【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件,零件尺寸均在[21.7,22.3](单位:cm)之间的零件,把零件尺寸在[21.9,22.1)的记为一等品,尺寸在[21.8,21.9)![]() [22.1,22.2)的记为二等品,尺寸在[21.7,21.8)
[22.1,22.2)的记为二等品,尺寸在[21.7,21.8)![]() [22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
[22.2,22.3]的记为三等品,现从甲、乙工艺生产的零件中各随机抽取100件产品,所得零件尺寸的频率分布直方图如图所示:
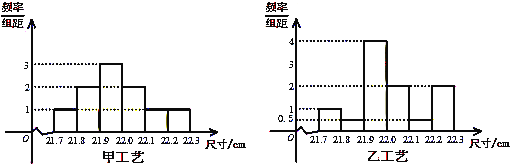
(Ⅰ)根据上述数据完成下列2×2列联表,根据此数据你认为选择不同的工艺与一等品产出率是否有关?
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
P(K2≥k) | 0.1 | 0.05 | 0.01 |
k | 2.706 | 3.841 | 6.635 |
附:![]() ,其中
,其中![]() .
.
(Ⅱ)以上述两种工艺中各种产品的频率作为相应产品产出的概率,若一等品、二等品、三等品的单件利润分别为30元、20元、15元,从一件产品的平均利润考虑,你认为以后该工厂应该选择哪种工艺生产该种零件?请说明理由.