题目内容

如图，四棱锥P-ABCD中，底面ABCD 为矩形，AB=8，AD=4 $数学公式$ ，侧面PAD为等边三角形，并且与底面所成二面角为60°．
（Ⅰ）求二面角A-PB-C的大小；
（Ⅱ）计算点A到面PBC的距离．

解：（Ⅰ）取AD的中点E，过E作AB的平行线交BC于F，再过P作PO垂直于面ABCD，易知PO交EF于O，则以O为原点，过O平行于EA的直线为x轴，OF所在直线为y轴，OP所在直线为z轴，建立空间直角坐标系．由已知AE= $\text{[math]}$ ，PE=6，∠PEO=60°，得PO=3 $\text{[math]}$ ，OE=3
∴ $\text{[math]}$
∴ $\text{[math]}$ ， $\text{[math]}$
设平面PAB的法向量为 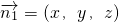$\text{[math]}$ ，则有 $\text{[math]}$ ，即 $\text{[math]}$
令z=1，得 $\text{[math]}$
设面PBC的法向量为 $\text{[math]}$ =（m，n，1），则有 $\text{[math]}$ ，即 $\text{[math]}$
∴ $\text{[math]}$
∴ $\text{[math]}$ 的夹角θ的余弦 $\text{[math]}$
则根据图形可知，所求二面角A-PB-C为钝二面角，故大小为 $\text{[math]}$ ．
（Ⅱ）点A到平面PBC的距离 $\text{[math]}$
分析：（Ⅰ）取AD的中点E，过E作AB的平行线交BC于F，再过P作PO垂直于面ABCD，以O为原点，过O平行于EA的直线为x轴，OF所在直线为y轴，OP所在直线为z轴，建立空间直角坐标系．从而可用坐标表示点，进而可得向量 $\text{[math]}$ ， $\text{[math]}$
的坐标，分别求出平面PAB的法向量 $\text{[math]}$ ，平面PBC的法向量 $\text{[math]}$ ，利用向量的夹角θ的余弦 $\text{[math]}$ ，可求二面角A-PB-C的大小．
（Ⅱ）利用点A到平面PBC的距离 $\text{[math]}$ 求解即可．
点评：本题以四棱锥为载体，考查面面角，考查点面距离，构建空间直角坐标系，利用向量的夹角公式，点面距离公式求解时解题的关键