题目内容
在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个,则实数t的取值范围为 .
【答案】分析:先在R上求解不等式|x3-3x+1|≥1,然后根据不等式的解集确定“在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个”t的范围.
解答:解:不等式|x3-3x+1|≥1?x3-3x+1≥1 ①或x3-3x+1≤-1 ②
解①得-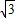 ≤x≤0或x
≤x≤0或x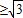
解②得x≤-2或x=1
∴不等式|x3-3x+1|≥1的解集为{x|x≤-2或-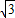 ≤x≤0或x
≤x≤0或x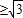 或x=1}
或x=1}
∵在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个
∴0<t<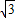 -1
-1
故答案为:(0,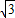 -1)
-1)
点评:在解不等式的过程中应用了因式分解求解不等式,增加了题目的难度,属中档题.
解答:解:不等式|x3-3x+1|≥1?x3-3x+1≥1 ①或x3-3x+1≤-1 ②
解①得-
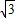 ≤x≤0或x
≤x≤0或x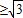
解②得x≤-2或x=1
∴不等式|x3-3x+1|≥1的解集为{x|x≤-2或-
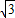 ≤x≤0或x
≤x≤0或x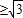 或x=1}
或x=1}∵在区间[t,t+1]上满足不等式|x3-3x+1|≥1的解有且只有一个
∴0<t<
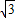 -1
-1故答案为:(0,
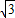 -1)
-1)点评:在解不等式的过程中应用了因式分解求解不等式,增加了题目的难度,属中档题.

练习册系列答案
相关题目
 x3+
x3+ x2-ax-a,x∈R,其中a>0.
x2-ax-a,x∈R,其中a>0.