题目内容
二次函数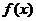
的图象顶点为
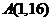，且图象在
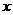轴上截得的线段长为8.
(Ⅰ)求函数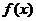的解析式；
（Ⅱ）令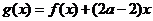
.
（ⅰ）求函数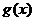
在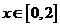
上的最小值；
（ⅱ）若
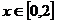时，不等式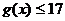
恒成立，试求实数
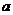的取值范围.
【答案】
解：(1)由题意设
，与
轴的交点坐标为
∴
∵
，由韦达定理可得
.
∴
,
∴
∴
(2) 
（ⅰ）当
时，
；
当
时，
．
（ⅱ）①当
时，
恒成立，只需
，即
，显然成立，∴.
②当
时，恒成立，只需
，即
，即
，∴
.
③当
时，恒成立，只需
，即
，即
，
这与
矛盾，故舍去．
综上所述，
的取值范围是
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
二次函数的图象顶点为A（1，16），且图象在x轴上截得的线段长8．
（1）求这个二次函数的解析式；
（2）在区间[-1，1]上，y=f （x）的图象恒在一次函数y=2x+m的图象上方，试确定实数m的范围．
（1）求这个二次函数的解析式；
（2）在区间[-1，1]上，y=f （x）的图象恒在一次函数y=2x+m的图象上方，试确定实数m的范围．
的图象顶点为
，且图象在
轴上截得线段长为8，则函数