题目内容
如图2-3-1,在正方体ABCD—A1B1C1D1中,P为DD1的中点,O为ABCD的中心,求证:B1O⊥平面PAC.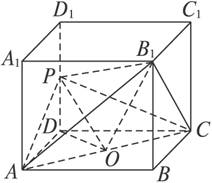
图2-3-1
思路分析:要证B1O⊥平面PAC,只需证B1O垂直于平面PAC中的两条相交直线.
证明:连结AB1、CB1,设AB=1.
因为AB1=CB1=![]() ,AO=CO,所以B1O⊥AC.连结PB1.
,AO=CO,所以B1O⊥AC.连结PB1.
因为OB12=OB2+BB12=![]() ,PB12=PD12+B1D12=
,PB12=PD12+B1D12=![]() ,OP2=PD2+DO2=
,OP2=PD2+DO2=![]() ,
,
所以OB12+OP2=PB12.
所以B1O⊥PO.所以B1O⊥平面PAC.
绿色通道:线面垂直可转化为线线垂直.应用勾股定理的逆定理,通过计算得出垂直也是证明垂直的常用手段.

练习册系列答案
相关题目

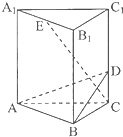 如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是3,D是侧棱CC1上一点且C1D=2DC,E是A1B1的中点.
如图所示,在正三棱柱ABC-A1B1C1中,底面边长和侧棱长都是3,D是侧棱CC1上一点且C1D=2DC,E是A1B1的中点.
