题目内容
(2013•和平区二模)已知双曲线
-y2=1的左、右焦点分别为F1、F2,点P在双曲线上,且PF2⊥x轴,则F2到直线PF1的距离为
.
| x2 |
| 3 |
| 4 |
| 7 |
| 4 |
| 7 |
分析:依题意,可求得点P的坐标,继而可求得直线PF1的方程,利用点到直线间的距离公式即可求得答案.
解答:解:∵F1、F2分别为双曲线
-y2=1的左、右焦点,
∴F1(-2,0),F2(2,0);
又点P在双曲线上,且PF2⊥x轴,
∴点P的横坐标为2,纵坐标y0=±
=±
.
∴P(2,±
).
∴直线PF1的方程为:
x±12y+2
=0.
∴F2到直线PF1的距离d=
=
.
故答案为:
.
| x2 |
| 3 |
∴F1(-2,0),F2(2,0);
又点P在双曲线上,且PF2⊥x轴,
∴点P的横坐标为2,纵坐标y0=±
|
| ||
| 3 |
∴P(2,±
| ||
| 3 |
∴直线PF1的方程为:
| 3 |
| 3 |
∴F2到直线PF1的距离d=
|
| ||||
7
|
| 4 |
| 7 |
故答案为:
| 4 |
| 7 |
点评:本题考查双曲线的简单性质,考查直线的方程的确定与点到直线间的距离,求得直线PF1的方程是关键,考查分析与运算能力,属于中档题.

练习册系列答案
相关题目
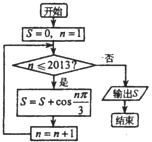 (2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( )
(2013•和平区二模)阅读如图所示的程序框图,运行相应的程序,则输出的结果S的值为( ) (2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )
(2013•和平区二模)已知函数y=Asin(ωx+φ)(A>0,ω>0),|φ|<π)的部分图象如图所示,则它的解析式为( )