题目内容
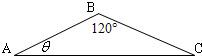已知△ABC中，|| AC |
| AB |
| BC |
（I）求f（θ）关于θ的表达式；
（II）求f（θ）的值域．
分析：（I）利用三角形的正弦定理求出三角形的边AB，BC，利用向量的数量积公式及和三角函数的和、差角公式表示出f（θ）．
（II）先求出角2θ+
，再利用三角函数的图象求出sin(2θ+
)，求出f（θ）的值域．
（II）先求出角2θ+
| π |
| 6 |
| π |
| 6 |
解答：解：（I）由正弦定理有：
=
=
；
∴|BC|=
sinθ，|AB|=
；
∴f（θ）=
•
=
sinθ•sin(600-θ)•
=
(
cosθ-
sinθ)sinθ=
sin(2θ+
)-
(0＜θ＜
)
（II）由0＜θ＜
?
＜2θ+
＜
；
∴
＜sin(2θ+
)≤1；
∴f（θ）∈(0，
]
| |BC| |
| sinθ |
| 1 |
| sin1200 |
| |AB| |
| sin(600-θ) |
∴|BC|=
| 1 |
| sin1200 |
| sin(600-θ) |
| sin1200 |
∴f（θ）=
| AB |
| BC |
| 4 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| π |
| 6 |
| 1 |
| 6 |
| π |
| 3 |
（II）由0＜θ＜
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴
| 1 |
| 2 |
| π |
| 6 |
∴f（θ）∈(0，
| 1 |
| 6 |
点评：本题考查三角函数的正弦定理、三角函数的和差角公式、向量的数量积公式、整体思想求三角函数的值域．
练习册系列答案
相关题目