题目内容
已知f(x)=ax2+x-a,a∈R.
(1)若a=1,解不等式f(x)≥1;
(2)若不等式f(x)>-2x2-3x+1-2a对一切实数x恒成立,求实数a的取值范围;
(3)若a<0,解不等式f(x)>1.
解:(1)当a=1,不等式f(x)≥1即 x2+x-1≥1,即(x+2)(x-1)≥0,解得 x≤-2,或 x≥1,故不等式的解集为{x|x≤-2,或 x≥1}.
(2)由题意可得 (a+2)x2+4x+a-1>0恒成立,当a=-2 时,显然不满足条件,∴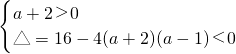 .
.
解得 a<2,故a的范围为(-∞,2).
(3)若a<0,不等式为 ax2+x-a-1>0,即 (x-1)(x+ )<0.
)<0.
∵1- =
=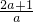 ,
,
∴当- <a<0时,1<-
<a<0时,1<- ,不等式的解集为 {x|-1<x<-
,不等式的解集为 {x|-1<x<- };
};
当 a=- 时,1=-
时,1=- ,不等式即(x-1)2<0,它的解集为∅;
,不等式即(x-1)2<0,它的解集为∅;
当a<- 时,1>-
时,1>- ,不等式的解集为 {x|-
,不等式的解集为 {x|- <x<1}.
<x<1}.
分析:(1)当a=1,不等式即(x+2)(x-1)≥0,解此一元二次不等式求得它的解集.
(2)由题意可得 (a+2)x2+4x+a-1>0恒成立,当a=-2 时,显然不满足条件,故有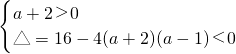 ,由此求得a的范围.
,由此求得a的范围.
(3)若a<0,不等式为 ax2+x-a-1>0,即 (x-1)(x+ )<0.再根据1和-
)<0.再根据1和- 的大小关系,求得此不等式的解集.
的大小关系,求得此不等式的解集.
点评:本题主要考查一元二次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.
(2)由题意可得 (a+2)x2+4x+a-1>0恒成立,当a=-2 时,显然不满足条件,∴
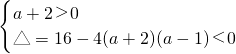 .
.解得 a<2,故a的范围为(-∞,2).
(3)若a<0,不等式为 ax2+x-a-1>0,即 (x-1)(x+
 )<0.
)<0.∵1-
 =
=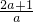 ,
,∴当-
 <a<0时,1<-
<a<0时,1<- ,不等式的解集为 {x|-1<x<-
,不等式的解集为 {x|-1<x<- };
}; 当 a=-
 时,1=-
时,1=- ,不等式即(x-1)2<0,它的解集为∅;
,不等式即(x-1)2<0,它的解集为∅;当a<-
 时,1>-
时,1>- ,不等式的解集为 {x|-
,不等式的解集为 {x|- <x<1}.
<x<1}.分析:(1)当a=1,不等式即(x+2)(x-1)≥0,解此一元二次不等式求得它的解集.
(2)由题意可得 (a+2)x2+4x+a-1>0恒成立,当a=-2 时,显然不满足条件,故有
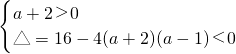 ,由此求得a的范围.
,由此求得a的范围.(3)若a<0,不等式为 ax2+x-a-1>0,即 (x-1)(x+
 )<0.再根据1和-
)<0.再根据1和- 的大小关系,求得此不等式的解集.
的大小关系,求得此不等式的解集.点评:本题主要考查一元二次不等式的解法,函数的恒成立问题,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目