题目内容
18．100件产品中有5件次品，不放回地抽取两次，每次抽1件，已知第一次抽出的是次品，则第2次抽出正品的概率为（ ）| A． | $\frac{19}{20}$ | B． | $\frac{19}{400}$ | C． | $\frac{1}{20}$ | D． | $\frac{95}{99}$ |
分析 根据题意，易得在第一次抽到次品后，有4件次品，95件正品，由概率计算公式，计算可得答案．
解答 解：根据题意，在第一次抽到次品后，有4件次品，95件正品；
则第二次抽到正品的概率为P=$\frac{95}{99}$，
故选：D．
点评 本题考查概率的计算，解题时注意题干“在第一次抽到次品条件下”的限制．
练习册系列答案
相关题目
8．已知锐角α，β满足sinα=$\frac{2\sqrt{5}}{5}$，cosβ=$\frac{\sqrt{10}}{10}$，则α+β=（ ）
| A． | $\frac{π}{4}$ | B． | $\frac{3}{4}$π | C． | $\frac{π}{4}$或$\frac{3}{4}$π | D． | $\frac{π}{2}$ |
6．过曲线y=x3+bx+c上一点A（1，2）的切线方程为y=x+1，则bc的值为（ ）
| A． | -6 | B． | 6 | C． | -4 | D． | 4 |
13．
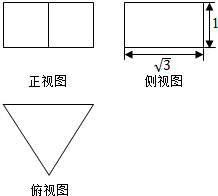若正三棱柱（底面为正三角形，且侧棱与底面垂直的三棱柱）的三视图如图所示，该三棱柱的表面积是（ ）
若正三棱柱（底面为正三角形，且侧棱与底面垂直的三棱柱）的三视图如图所示，该三棱柱的表面积是（ ）| A． | $\sqrt{3}$ | B． | 6+2$\sqrt{3}$ | C． | 6+$\sqrt{3}$ | D． | $\frac{9\sqrt{3}}{2}$ |
3．A={1，2，3}，B={-1，2，-3}，A∩B=（ ）
| A． | {2} | B． | 2 | C． | {-3，-1，1，2，3} | D． | φ |
10．甲、乙、丙三人独立地去译一个密码，分别译出的概率为$\frac{1}{5}$，$\frac{1}{3}$，$\frac{1}{4}$，则此密码能译出的概率是（ ）
| A． | $\frac{1}{60}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{59}{60}$ |