题目内容
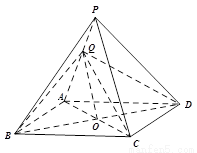
(本小题满分13分)如图所示,四棱锥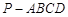 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,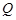 是棱
是棱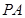 上的动点.
上的动点.
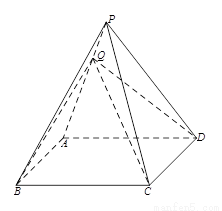
(Ⅰ)若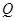 是
是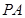 的中点,求证:
的中点,求证: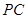 //平面
//平面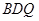 ;
;
(Ⅱ)若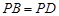 ,求证:
,求证: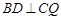 ;
;
(III)在(Ⅱ)的条件下,若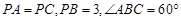 ,求四棱锥
,求四棱锥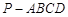 的体积.
的体积.
【答案】
(1)根据底面 为菱形, 所以
为菱形, 所以 为
为 的中点.
的中点.
因为 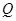 是
是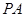 的中点,所以
的中点,所以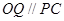 从而得证。
从而得证。
(2)根据已知的条件得到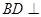 平面
平面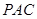 ,然后结合线面垂直的性质定理得到结论
,然后结合线面垂直的性质定理得到结论
(3)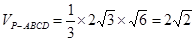
【解析】
试题分析:(Ⅰ)证明:连结 ,交
,交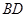 于
于 .
.
因为底面 为菱形, 所以
为菱形, 所以 为
为 的中点.
的中点.
因为 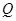 是
是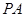 的中点,所以
的中点,所以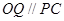 ,
,
因为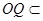 平面
平面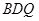 ,
,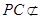 平面
平面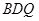 ,
,
所以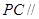 平面
平面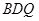 . …………………4分
. …………………4分
(Ⅱ)证明:因为底面 为菱形,
为菱形,
所以 ,
, 为
为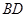 的中点.
的中点.
因为 ,所以
,所以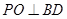 .
.
因为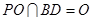 ,所以
,所以 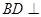 平面
平面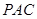 .因为
.因为 平面
平面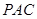 ,
,
所以  . ………………………………8分
. ………………………………8分
(Ⅲ)因为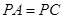 ,所以△
,所以△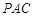 为等腰三角形 .
为等腰三角形 .
因为 为
为 的中点,所以
的中点,所以 .
.
由(Ⅱ)知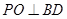 ,且
,且 ,
,
所以 平面
平面 ,即
,即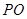 为四棱锥
为四棱锥 的高.
的高.
因为四边形是边长为2的菱形,且 ,
,
所以
 .
.
所以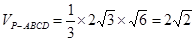 . ……………12分
. ……………12分
考点:线面平行,线线垂直,体积的问题
点评:解决该试题的关键是利用空间的线面平行和线面垂直的性质定理和判定定理来证明平行与垂直同时根据等体积法来求解体积。属于中档题。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目

 .
. 的最小正周期和最大值;
的最小正周期和最大值; 在区间
在区间 上的图象.
上的图象. ,且方程
,且方程 有两个不同的实数根,求实数m的取值范围.
有两个不同的实数根,求实数m的取值范围. 的函数
的函数 是奇函数.
是奇函数. 的值;(2)判断函数
的值;(2)判断函数 的单调性;
的单调性; ,不等式恒成立
,不等式恒成立 ,求k的取值范围.
,求k的取值范围. ,
,  ,
, .
. (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范围.
的取值范围. 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

 为锐角,且
为锐角,且 ,函数
,函数 ,数列{
,数列{ }的首项
}的首项 .
. 的表达式;
的表达式; 中,若
中,若 A=2
A=2 ,BC=2,求
,BC=2,求 的前
的前 项和
项和