题目内容
如图，已知四棱锥P—ABCD中，底面ABCD为正方形，侧面PDC为正三角形，且平面PDC⊥底面ABCD，E为PC的中点，求证：PA∥平面 BDE.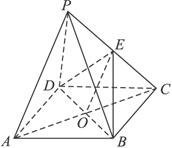
证明：连结AC交BD于O，
又E为PC的中点，∴PA∥OE.
而OE
平面BDE，PA
平面BDE，
∴PA∥平面BDE.
练习册系列答案
相关题目
题目内容
如图，已知四棱锥P—ABCD中，底面ABCD为正方形，侧面PDC为正三角形，且平面PDC⊥底面ABCD，E为PC的中点，求证：PA∥平面 BDE.
证明：连结AC交BD于O，
又E为PC的中点，∴PA∥OE.
而OE平面BDE，PA平面BDE，
∴PA∥平面BDE.
如图：已知四棱锥P-ABCD中，PD⊥平面ABCD，ABCD是正方形，E是PA的中点，
如图，已知四棱锥P-ABCD，底面ABCD为菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
如图，已知四棱锥P-ABCD的底面为菱形，∠BCD=60°，PD⊥AD．点E是BC边上的中点．
（2012•崇明县二模）如图，已知四棱锥P-ABCD的底面ABCD为正方形，PA⊥平面ABCD，E、F分别是BC，PC的中点，AB=2，AP=2．
（2012•吉林二模）如图，已知四棱锥P-ABCD的底面是正方形，PA⊥面ABCD，且PA=AD=2，点M，N分别在PD，PC上，