题目内容
设甲、乙两名射手各打了5发子弹，每发子弹击中环数如下：
甲：10， 6， 8， 7, 9
乙：8， 9， 9， 7， 7
根据已学的统计知识，从总体水平和稳定性两方面考虑，甲、乙两名射手的射击技术评定情况是（ ）
| A．甲比乙好 | B．乙比甲好 | C．甲、乙一样好 | D．难以确定 |
B
解析试题分析： 先做出两组数据的平均数，发现平均数相等，从平均数上不能区分两组数据的好坏，又求两组数据的方差，从稳定程度上来比较两个人的技术好坏，得到乙的水平较高。
因为
，而利用均值可知S2甲>S2乙，从而说明乙比甲好，选B.
考点：本题主要考查了两组数据的平均数和方差，来判断两个人的射击水平好坏，本题是一个统计部分经常出现的一个问题，本题由于数据运算比较困难，是一个易错题．
点评：解决该试题的关键是比较水平的高低主要是看平均值，平均值相同的情况下，再看那方差的大小来得到。
某班主任对全班50名学生进行了作业量多少的调查，数据如下表：
| | 认为作业多 | 认为作业不多 | 总数 |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
. | 0.050 | 0.025 | 0.010 | 0.001 |
 | 3.841 | 5.024 | 6.635 | 10.828 |
参照附表，得到的正确结论是
A.有
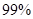的把握认为“喜欢玩电脑游戏与认为作业量的多少有关系”;B.有
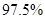的把握认为“喜欢玩电脑游戏与认为作业量的多少无关系”;C.在犯错误的概率不超过
的前提下，认为“喜欢玩电脑游戏与认为作业量的多少无关系”;D.在犯错误的概率不超过
的前提下，认为“喜欢玩电脑游戏与认为作业量的多少有关系”. 已知随机事件A与B，经计算得到
的范围是3.841＜＜6.635，则（下表是的临界值表，供参考）
P( ≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A. 有95% 把握说事件A与B有关 B. 有95% 把握说事件A与B无关
C. 有99% 把握说事件A与B有关 D. 有99% 把握说事件A与B无关
某单位有职工100人，其中青年人有45人，中年人有25人，剩下的为老年人，用分层抽样的方法从中抽取20人，则各年龄段分别抽取多少人（ ）
| A．7，5，8 | B．9，5，6 | C．6，5，9 | D．8，5，7 |
某商场在国庆黄金周的促销活动中，对10月2日9时至14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为2.5万元，则11时至12时的销售额为（ ）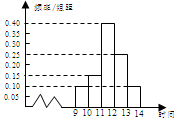
| A．6万元 | B．8万元 | C．10万元 | D．12万元 |
已知一组正数
的方差为
，则数据
的平均数为（ ）
| A．2 | B．3 | C．4 | D．6 |
已知一组数据
的平均数是2，方差是
，那么另一组数据
的平均数和方差分别为（ ）
| A．2， | B．4，3 | C．4， | D．2，1 |
为调查参加运动会的1000名运动员的年龄情况，从中抽查了100名运动员的年龄，就这个问题来说，下列说法正确的是( )
| A．1000名运动员是总体 |
| B．每个运动员是个体 |
| C．抽取的100名运动员是样本 |
| D．样本容量是100 |