题目内容
在四棱锥 中,平面
中,平面 平面
平面 ,
, ,在锐角
,在锐角

 中
中 ,并且
,并且 ,
,
(1)点 是
是 上的一点,证明:平面
上的一点,证明:平面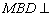 平面
平面 ;
;
(2)若 与平面
与平面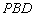 成角
成角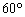 ,当面
,当面 平面
平面 时,
时,
求点 到平面
到平面 的距离.
的距离.
解法一(1)因为 ,
, ,由勾股定理得
,由勾股定理得 ,因为平面
,因为平面 平面
平面 ,平面
,平面 平面
平面 =
= ,
, 面
面 ,所以
,所以 平面
平面
 面
面 ,所以平面
,所以平面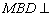 平面
平面 ………6分
………6分
 (2)如图,因为
(2)如图,因为 平面
平面 ,所以平面
,所以平面 平面
平面 ,所以
,所以 ,做
,做 于
于 ,所以
,所以 面
面 ,
, ,设面
,设面 面
面 =
= ,面
,面 平面
平面 所以面
所以面 面
面 ,所以
,所以 ,取
,取 中点
中点 ,得
,得 为平行四边形,由平面
为平行四边形,由平面 边长得
边长得 为
为 中点,所以
中点,所以 ………12分
………12分
解法二(1)同一
(2)在平面 过
过 做
做 垂线为
垂线为 轴,由(1),以
轴,由(1),以 为原点,
为原点, 为
为 轴建立空间直角坐标系,设平面
轴建立空间直角坐标系,设平面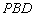 法向量为
法向量为 ,设
,设 ,锐角
,锐角 所以
所以 ,由
,由 ,解得
,解得 ,
, ,
, ,解得
,解得 或
或 (舍)
(舍)
设 ,解得
,解得
因为面 平面
平面 ,
, ,所以面
,所以面 法向量为
法向量为 ,所以
,所以 ,解得
,解得 ,所以
,所以 到平面
到平面 的距离为竖坐标
的距离为竖坐标 . ………12分
. ………12分

练习册系列答案
相关题目
 上有一动点
上有一动点 ,圆
,圆 ,过圆心
,过圆心 任意作一条直线与圆
任意作一条直线与圆 和
和 ,圆
,圆 ,过圆心
,过圆心 任意作一条直线与圆
任意作一条直线与圆 和
和 ,则
,则 的最小值为 。
的最小值为 。 = .
= .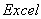 中产生
中产生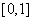 区间上均匀随机数的函数为“
区间上均匀随机数的函数为“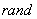 ( )”,在用计算机模拟估计函数
( )”,在用计算机模拟估计函数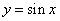 的图像、直线
的图像、直线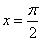 和
和 轴在区间
轴在区间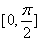 上部分围成的图形面积时,随机点
上部分围成的图形面积时,随机点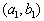 与该区域内的点
与该区域内的点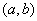 的坐标变换公式为 ( )
的坐标变换公式为 ( )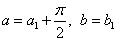 B.
B. 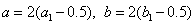
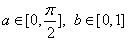 D.
D. 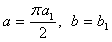
 满足
满足 ,
, ,则该数列的前
,则该数列的前 项的乘积 .
项的乘积 . 以上的把握认为这个结论是成立的。下列说法中正确的是( )
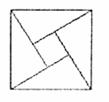
以上的把握认为这个结论是成立的。下列说法中正确的是( )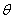 ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是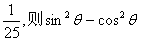 的值等于
的值等于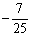 C.
C.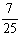 D.
D.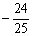
 的图象
的图象 个单位 B、向右平移
个单位 B、向右平移 个单位
个单位