题目内容
设x,y是非零实数,“
>
”是“
<
”的( )
| x |
| y |
| 1 |
| x |
| 1 |
| y |
分析:分别从充分性和必要性两方面加以论证:根据二次根式的性质和不等式变形的法则,可得到充分性成立,再通过举反例说明必要性不成立.由此可得正确选项.
解答:解:先看充分性
若“
>
”成立,说明x>y≥0
再结合已知条件x,y是非零实数,得x>y>0
两边都除以正数xy,得
>
>0⇒“
<
”,故充分性成立
再看必要性
若“
<
”成立,有可能x<0<y,
不能得到“
>
”成立,因此没有必要性
综上所述,“
>
”是“
<
”的充分不必要条件
故选A
若“
| x |
| y |
再结合已知条件x,y是非零实数,得x>y>0
两边都除以正数xy,得
| 1 |
| y |
| 1 |
| x |
| 1 |
| x |
| 1 |
| y |
再看必要性
若“
| 1 |
| x |
| 1 |
| y |
不能得到“
| x |
| y |
综上所述,“
| x |
| y |
| 1 |
| x |
| 1 |
| y |
故选A
点评:本题以不等式的同解变形为例,考查了充分必要条件的判断,属于基础题.充分理解不等式的基本性质和充分必要条件的含义是解决本题的关键.

练习册系列答案
相关题目
 >
>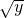 ”是“
”是“ <
< ”的
”的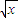 >
>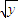 ”是“
”是“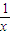 <
<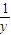 ”的( )
”的( )