Question

函数f（x）=|lgx|+x-2的零点个数是

2

．

Answer 1

分析：函数f（x）=|lgx|+x-2的零点可转化成f（x）=0根的个数，然后转化成函数y=|lgx|与函数y=2-x的交点的个数，作出函数y=2-x与函数y=|lgx|的图象，结合函数的图判断即可．

解答：解：f（x）=0?|lgx|=2-x，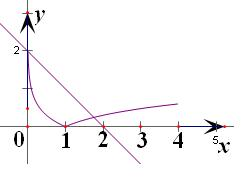
所以f（x）的零点个数即函数y=|lgx|与函数y=2-x的交点的个数，
作出函数y=2-x与函数y=|lgx|的图象，结合函数的图可知有2个交点，
故答案为：2．

点评：本题主要考查了函数的零点的个数的判断，同时考查了转化的数学思想，解题的关键是准确作出函数的图象，属于基础试题．