题目内容
(本小题满分10分)
四棱锥P-ABCD中,底面ABCD是正方形,
边长为 ,PD=
,PD= ,PD⊥平面ABCD
,PD⊥平面ABCD
(1)求证: AC⊥PB ;
(2)求二面角A-PB-D的大小;
(3)求四棱锥外接球的半径.
(4)在这个四棱锥中放入一个球,求球的最大半径;

【答案】
(1)证明
(2) A-PB-D的大小为60
(3) 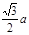
(4)球的最大半径为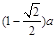
【解析】(1)证明:连结BD,∵ABCD是正方形∴BD⊥AC ∵PD⊥平面ABCD∴PD⊥AC
∵PD∩BD=D ∴AC⊥平面PDB∵PBÌ平面PDB ∴AC⊥PB ……………(4分)
(2)解:设AC∩BD=0,过A作AE⊥PB于E,连接OE∵AO⊥平面PBD ∴OE⊥PB
∴∠AEO为二面角 A-PB-D的平面角∵PD⊥平面ABCD,AD⊥AB
∴PA⊥AB在Rt△PDB中,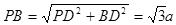 ,在Rt△PAB中,
,在Rt△PAB中,
∵ ∴
∴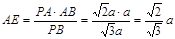 ,
,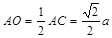
在Rt△AOE中,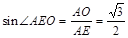 ,∴∠AEO=60°
,∴∠AEO=60°
∴二面角A-PB-D的大小为60. ……………(8分)
(3)解:解:设PB的中点为F,∵在Rt△PDB中:FP=FB=FD
在Rt△PAB中:FA=FP=FB,在Rt△PBC中:FP=FB=FC
∴FP=FB=FA=FC=FD ∴F为四棱锥外接球的球心
则FP为外接球的半径 ∵FP= ∴
∴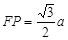
∴四棱锥外接球的半径为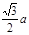 ……………(12分)
……………(12分)
(4) 设此球半径为R,最大的球应与四棱锥各个面都相切,设球心为S,连SA、SB、SC、SD、SP,则把此四棱锥分为五个棱锥,设它们的高均为R
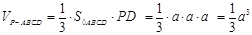

∵ 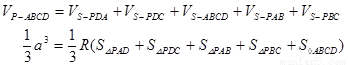
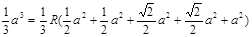
∴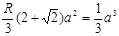 ∴
∴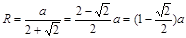
∴球的最大半径为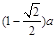

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 (选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤.
(选做题)本题包括A、B、C、D四小题,请选定其中两题,并在答题卡指定区域内作答,若多做,则按作答的前两题评分,解答时应写出文字说明、证明过程或演算步骤. 本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,
本题包括(1)、(2)、(3)、(4)四小题,请选定其中两题,并在答题卡指定区域内答,