题目内容
若函数f(x)=2|x-3|+logax+1无零点,则a的取值范围为________.

分析:把函数的零点转化为两函数图象的交点,利用图象直接得结论.
解答:
 解:∵函数f(x)=2|x-3|+logax+1无零点,
解:∵函数f(x)=2|x-3|+logax+1无零点,∴y=2|x-3|与y=logax-1的图象无交点,
在同一坐标系中画出函数,
当0<a<1时,两个函数图象有交点,因此不符合题意;
当a>1时,∵函数f(x)=2|x-3|-logax+1无零点,
∴-1+loga3<1,解得a
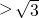 ,
,∴的取值范围为
 ,
,故答案为
 .
.点评:本题考查了利用函数零点的存在性求变量的取值范围.是道中档题.

练习册系列答案
相关题目
若函数f(x)=2-|x|-x2+a有两个不同的零点,则实数a的取值范围是( )
| A、[1,+∞) | B、(1,+∞) | C、[-1,+∞) | D、(-1,+∞) |