题目内容
【题目】从某市统考的学生数学考试卷中随机抽查100份数学试卷作为样本，分别统计出这些试卷总分，由总分得到如下的频率分别直方图.
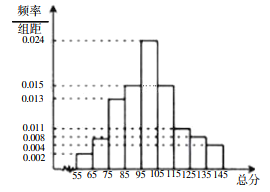
（1）求这100份数学试卷成绩的中位数；
（2）从总分在
和
的试卷中随机抽取2份试卷，求抽取的2份试卷中至少有一份总分少于65分的概率.
【答案】（1）100； （2）
.
【解析】
（1）通过左边起，频率和为
的位置即为中位数的位置.
的试卷有
份和
的试卷有
份，利用列举法求得基本事件的总数，从中得到至少有一份总分少于
的事件的个数，由此计算得概率.
（1）记这100份数学试卷成绩的中位数为
则
解得：
,所以，中位数为100.
（2）总分在共有
（份），记为
总分在的试卷共有
（份），记为
则从上述6份试卷中随机抽取2份的抽取结果为：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
共计15种结果，且每个结果是等可能的，
至少有一份总分少于65分的有：，，，，，，，，，共计9种结果，
所以抽取的2份至少有一份总分少于65分的概率
.
练习册系列答案
导学全程练创优训练系列答案
相关题目
