题目内容
若函数f(x)=-x+2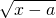 的单调递增区间为[0,1],则a=________.
的单调递增区间为[0,1],则a=________.
0
分析:由f(x)=-x+2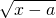 ,知
,知 ,由
,由 >0,函数f(x)=-x+2
>0,函数f(x)=-x+2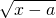 的单调递增区间为[0,1],能求出a.
的单调递增区间为[0,1],能求出a.
解答:∵f(x)=-x+2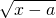 ,
,
∴ ,
,
由 >0,
>0,
得 ,
,
∴0<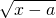 <1,
<1,
解得a<x<a+1,
∵函数f(x)=-x+2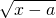 的单调递增区间为[0,1],
的单调递增区间为[0,1],
∴a=0,
故答案为:0.
点评:本题考查利用导数研究函数的单调性的应用,解题时要认真审题,注意导数的性质在求函数增区间时的灵活运用.
分析:由f(x)=-x+2
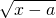 ,知
,知 ,由
,由 >0,函数f(x)=-x+2
>0,函数f(x)=-x+2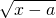 的单调递增区间为[0,1],能求出a.
的单调递增区间为[0,1],能求出a.解答:∵f(x)=-x+2
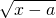 ,
,∴
 ,
,由
 >0,
>0,得
 ,
,∴0<
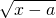 <1,
<1,解得a<x<a+1,
∵函数f(x)=-x+2
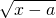 的单调递增区间为[0,1],
的单调递增区间为[0,1],∴a=0,
故答案为:0.
点评:本题考查利用导数研究函数的单调性的应用,解题时要认真审题,注意导数的性质在求函数增区间时的灵活运用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
若函数f(x)(x∈R)为奇函数,且存在反函数f-1(x)(与f(x)不同),F(x)=
,则下列关于函数F(x)的奇偶性的说法中正确的是( )
| 2f(x)-2f-1(x) |
| 2f(x)+2f-1(x) |
| A、F(x)是奇函数非偶函数 |
| B、F(x)是偶函数非奇函数 |
| C、F(x)既是奇函数又是偶函数 |
| D、F(x)既非奇函数又非偶函数 |