题目内容
已知f′(x)是f(x)的导函数,f(x)=ln(x+1)+m﹣2f′(1),m∈R,且函数f(x)的图象过点(0,-2).
(1)求函数y=f(x)的表达式;
(2)设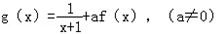 ,若g(x)>0在定义域内恒成立,求实数a的取值范围.
,若g(x)>0在定义域内恒成立,求实数a的取值范围.
(1)求函数y=f(x)的表达式;
(2)设
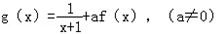 ,若g(x)>0在定义域内恒成立,求实数a的取值范围.
,若g(x)>0在定义域内恒成立,求实数a的取值范围.解:(1)由已知得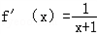 ,
,
∴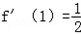
又f(0)=﹣2
∴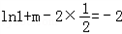
∴m=﹣1,
∴f(x)=ln(x+1)﹣2.
(2)由(1)得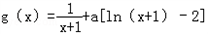
定义域为(﹣1,+∞),
∴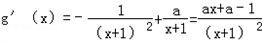 .
.
∵a≠0
令g'(x)=0得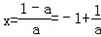
①当a>0时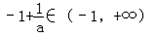 ,
,
且在区间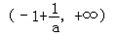 上g′(x)>0,在区
上g′(x)>0,在区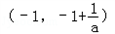 上g′(x)<0.∴
上g′(x)<0.∴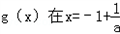 处取得极小值,也是最小值.
处取得极小值,也是最小值.
∴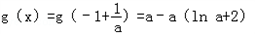
由a+a(﹣lna﹣2)>0得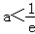 .∴
.∴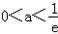 .
.
②当a<0时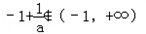 ,
,
在区间(﹣1,+∞)上,g′(x)<0恒成立.
g(x)在区间(﹣1,+∞)上单调递减,没有最值
综上得,a的取值范围是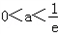 .
.
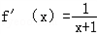 ,
,∴
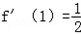
又f(0)=﹣2
∴
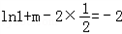
∴m=﹣1,
∴f(x)=ln(x+1)﹣2.
(2)由(1)得
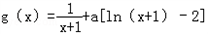
定义域为(﹣1,+∞),
∴
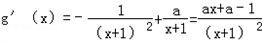 .
.∵a≠0
令g'(x)=0得
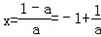
①当a>0时
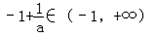 ,
,且在区间
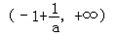 上g′(x)>0,在区
上g′(x)>0,在区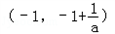 上g′(x)<0.∴
上g′(x)<0.∴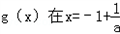 处取得极小值,也是最小值.
处取得极小值,也是最小值.∴
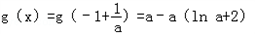
由a+a(﹣lna﹣2)>0得
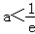 .∴
.∴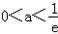 .
.②当a<0时
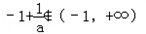 ,
,在区间(﹣1,+∞)上,g′(x)<0恒成立.
g(x)在区间(﹣1,+∞)上单调递减,没有最值
综上得,a的取值范围是
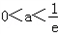 .
.
练习册系列答案
相关题目