题目内容
设函数 定义域为
定义域为 .
.
(1)若 ,求实数
,求实数 的取值范围;
的取值范围;
(2)若 在
在 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围.
(1)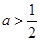 ,(2)
,(2)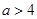 .
.
解析试题分析:(1)因为 ,所以
,所以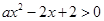 在
在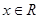 上恒成立. ① 当
上恒成立. ① 当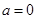 时,由
时,由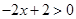 ,得
,得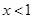 ,不成立,舍去,② 当
,不成立,舍去,② 当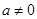 时,由
时,由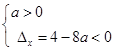 ,得
,得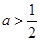 ,综上所述,实数
,综上所述,实数 的取值范围是
的取值范围是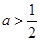 .(2))恒成立问题一般利用变量分离法转化为最值问题. 依题有
.(2))恒成立问题一般利用变量分离法转化为最值问题. 依题有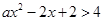 在
在 上恒成立,所以
上恒成立,所以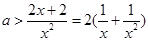 在
在 上恒成立, 令
上恒成立, 令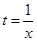 ,则由
,则由 ,得
,得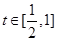 ,记
,记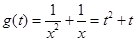 ,由于
,由于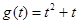 在
在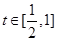 上单调递增, 所以
上单调递增, 所以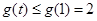 ,
, 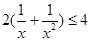
因此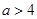
试题解析:解:(1)因为 ,所以
,所以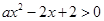 在
在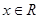 上恒成立. 2分
上恒成立. 2分
① 当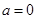 时,由
时,由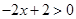 ,得
,得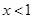 ,不成立,舍去, 4分
,不成立,舍去, 4分
② 当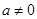 时,由
时,由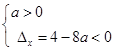 ,得
,得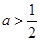 , 6分
, 6分
综上所述,实数 的取值范围是
的取值范围是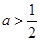 . 8分
. 8分
(2)依题有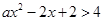 在
在 上恒成立, 10分
上恒成立, 10分
所以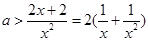 在
在 上恒成立, 12分
上恒成立, 12分
令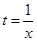 ,则由
,则由 ,得
,得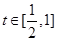 ,
,
记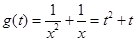 ,由于
,由于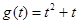 在
在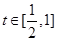 上单调递增,
上单调递增,
所以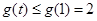 ,
, 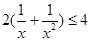
因此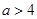 16分
16分
(使用函数在定义区间上最小值大于0求解可参照给分)
考点:不等式恒成立问题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 与时刻
与时刻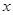 (时)的关系为
(时)的关系为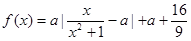 ,
, ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且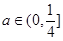 ,用每天
,用每天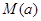 .
.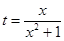 ,
,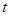 的取值范围;
的取值范围; 公里的相邻两增压站之间的输油管道费用为
公里的相邻两增压站之间的输油管道费用为 万元.设余下工程的总费用为
万元.设余下工程的总费用为 万元.
万元. (x∈R,且x≠2).
(x∈R,且x≠2). 的单调区间;
的单调区间;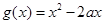 与函数
与函数 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值; 是边长为
是边长为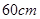 的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得
的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒, 在
在 上是被切去的等腰直角三角形斜边的两个端点,设
上是被切去的等腰直角三角形斜边的两个端点,设 .
. 最大,试问
最大,试问 应取何值?
应取何值? 最大,试问
最大,试问


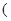 常数
常数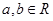 )满足
)满足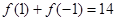 .
. 的值,并就常数
的值,并就常数 的不同取值讨论函数
的不同取值讨论函数 奇偶性;
奇偶性;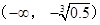 上单调递减,求
上单调递减,求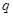 且存在递增的正整数数列
且存在递增的正整数数列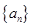 ,使得
,使得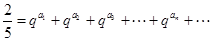 成立.
成立. 的单调递减区间是
的单调递减区间是