题目内容
(本小题满分12分)如图,已知平面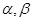 ,
,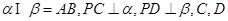 是垂足.
是垂足.
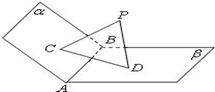
(Ⅰ)求证: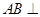 平面
平面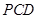 ;
;
(Ⅱ)若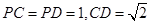 ,求证:
,求证: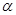
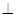
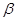 .
.
【答案】
(Ⅰ)见解析(Ⅱ)见解析
【解析】
试题分析:(Ⅰ)因为 ,所以
,所以 .
.
同理 .
.
又 ,
,
故 平面
平面 .
……4分.
.
……4分.
(Ⅱ)设 与平面
与平面 的交点为
的交点为 ,连结
,连结 、
、 .
.
因为 平面
平面 ,所以
,所以 ,
,
所以 是二面角
是二面角 的平面角.
的平面角.
又 ,
,
所以 ,即
,即 .
.
在平面四边形 中,
中, ,
,
所以 .故平面
.故平面 平面
平面 .
……12分
.
……12分
考点:本小题主要考查线面垂直和面面垂直的证明,考查了学生的空间想象能力和推理论证能力和划归思想的运用.
点评:垂直是立体几何的必考题目,且几乎每年都有一个解答题出现,所以是高考的热点也是重点.而灵活利用几何体的结构特征找出平面图形中的平行与垂直关系是证明的关键.

练习册系列答案
相关题目