题目内容
函数
 的图象恒过定点
的图象恒过定点 ,若点
,若点 在直线
在直线 上,其中
上,其中 ,则
,则 的最小值为 .
的最小值为 .
【答案】
 .
.
【解析】
试题分析:函数
 的图象恒过定点
的图象恒过定点 ,由对数函数的图象特征知A(-2,-1)代入
,由对数函数的图象特征知A(-2,-1)代入 得,
得, ,其中
,其中 ,
,
所以 =(
=( )(
)( )=4+
)=4+
 ,
,
故 的最小值为8.
的最小值为8.
考点:本题主要考查对数函数的图象,均值定理的应用。
点评:典型题,本题综合性较强,考查知识点多。利用已知条件得到 ,运用“1的代换”,创造了应用均值定理的条件。应用均值定理“一正、二定、三相等”。
,运用“1的代换”,创造了应用均值定理的条件。应用均值定理“一正、二定、三相等”。

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 的图象恒过定点A,若点A在直线
的图象恒过定点A,若点A在直线 上,其中
上,其中 ,则
,则 的最小值为 .
的最小值为 . (a>0,且a≠1),
(a>0,且a≠1), =
=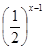 .
. 的图象恒过定点A,求A点坐标;
的图象恒过定点A,求A点坐标; 的图像过点(2,
的图像过点(2, ),证明:函数
),证明:函数 在
在 (1,2)上有唯一的零点.
(1,2)上有唯一的零点. 
 的图象恒过定点
的图象恒过定点 ,若点
,若点 上,其中
上,其中 均大于0,则
均大于0,则 的最大值为(
)
的最大值为(
) B.
B. C.
C. D.
D.

 的图象恒过定点
的图象恒过定点 ,若点
,若点 上,其中
上,其中 ,则
,则 的最小值为 ▲
的最小值为 ▲
 的图象恒过定点
的图象恒过定点 ,且点
,且点 上,若
上,若 ,则
,则 的最小值为
.
的最小值为
.