题目内容
设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足,如果直线AF的斜率为-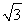
,那么|PF|等于( )
(A)4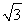 (B)8 (C)8 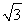(D)16
【答案】
B
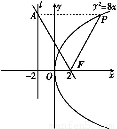
【解析】如图所示,直线AF的方程为y=-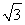
(x-2),与准线方程x=-2联立得A(-2,4).
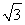设P(x0,4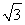),代入抛物线y2=8x,
得8x0=48,∴x0=6,
∴|PF|=x0+2=8,选B.
练习册系列答案
相关题目
设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，则直线l的斜率的取值范围是（ ）
A、[-
| ||||
| B、[-2，2] | ||||
| C、[-1，1] | ||||
| D、[-4，4] |
设抛物线y2=8x的焦点为F，过F，的直线交抛物线于A（x1，y1），B（x2，y2），则y1y2=（ ）
| A、8 | B、16 | C、-8 | D、-16 |