题目内容
已知M为椭圆上的一点，椭圆的两个焦点为F1、F2，且椭圆的长轴长为10，焦距为6，点I为△MF1F2的内心，延长线段MI交线段F1F2于N，则
的值为（ ）
| MI |
| IN |
分析：连接IF1、IF2，△MF1N中根据内角平分线定理，得
=
；同理在△MF2N中：
=
，再用椭圆定义和比例的基本性质得
=
=
，得到本题答案．
| |MF1| |
| |NF1| |
| |MI| |
| |IN| |
| |MF2| |
| |NF2| |
| |MI| |
| |IN| |
| |MI| |
| |IN| |
| 2a |
| 2c |
| 5 |
| 3 |
解答：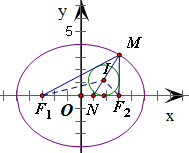
解：连接IF1、IF2，
∵I为△MF1F2的内心，
∴IF1平分∠MF1N，可得
=
同理可得：
=
，得
=
=
．
∴
=
∵M是椭圆上一点，且椭圆的长轴长为10
∴|MF1|+|MF2|=2a=10
而|NF1|+|NF2|=2c=6，可得
=
=
故选：D
解：连接IF1、IF2，∵I为△MF1F2的内心，
∴IF1平分∠MF1N，可得
| |MF1| |
| |NF1| |
| |MI| |
| |IN| |
同理可得：
| |MF2| |
| |NF2| |
| |MI| |
| |IN| |
| |MI| |
| |IN| |
| |MF1| |
| |NF1| |
| |MF2| |
| |NF2| |
∴
| |MI| |
| |IN| |
| |MF1|+|MF2| |
| |NF1|+|NF2| |
∵M是椭圆上一点，且椭圆的长轴长为10
∴|MF1|+|MF2|=2a=10
而|NF1|+|NF2|=2c=6，可得
| |MI| |
| |IN| |
| 2a |
| 2c |
| 5 |
| 3 |
故选：D
点评：本题给出椭圆焦点三角形的内心，求它的内角平分线MN被内心I分成的两段的比，着重考查了椭圆的定义与三角形内角平分线定理等知识，属于基础题．
练习册系列答案
相关题目
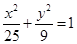上一点，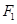
为椭圆的一个焦点，且
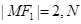为线段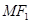
的中点，则ON的长为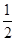 
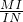上的一点，M，N分别为圆（x+3）2+y2=1和圆（x-3）2+y2=4上的点，则|PM|+|PN|的最小值为
的值为
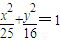上的一点，M，N分别为圆（x+3）2+y2=1和圆（x-3）2+y2=4上的点，则|PM|+|PN|的最小值为（ ）